Propriété du parallélogramme

Dans cette vidéo, on va illustrer la propriété du parallélogramme. Cette propriété nous inique comment additionner deux vecteurs partant de la même origine.

Avec le méthode de Chasles, nous avons appris à additionner des vecteurs qui sont mis bout à bout. Mais que faire quand ils ne le sont pas? On va se rappeler qu'un vecteur est défini par sa direction, son sens et sa longueur. Or deux vecteurs parallèles ont la même direction. Donc si on prend deux vecteurs parallèles ayant le même sens et la même longueur, ils représentent le même vecteur.

Prenons deux vecteurs quelconques $\vec{u}$ et $\vec{v}$, situés dans le plan (cf. dessin gauche ci-dessous). Si on déplace notre vecteur $\vec{v}$ jusqu'au bout de notre vecteur $\vec{u}$, tant que le vecteur $\vec{v}$ ne change pas de direction de sens ou de longueur, il reste le même vecteur, et on peut donc appliquer la relation de Chasles (cf dessin de droite ci-dessous) :

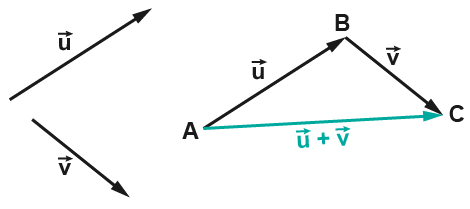
On a simplement déplacé le vecteur $\vec{v}$ en prenant soin de garder la même longueur, sens et direction. Ceci n'est que possible si on le fait de manière parallèle, c'est-à-dire notre vecteur $\vec{v}$ à gauche et celui à droite sont parallèles; s'ils ne l'étaient pas, ils n'auraient pas la même direction et ne représenteraient plus le même vecteur.

Maintenant imaginons qu'on veuille additionner les vecteurs $\vec{u} = \overrightarrow{AB}$ et $\vec{v} =\overrightarrow{AC}$. Il suffit de refaire la même méthode que précédemment: on va déplacer un des vecteurs de manière parallèle (traitillé orange sur le dessin ci-dessous), et ensuite on pourra appliquer Chasles pour faire l'addition:

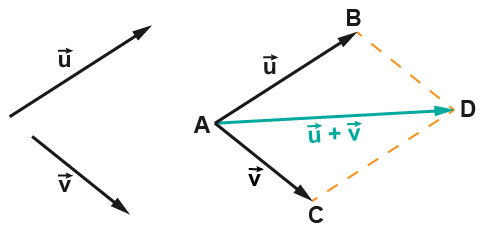
La figure résultante $ABCD$ est un parallélogramme. Pourquoi? Etant donné qu'on doit déplacer les vecteurs parallèlement pour qu'ils gardent la même direction, $\vec{u}$ et $\vec{v}$ et leur équivalent en traitillé orange sont parallèles. On se retrouve donc avec une figure qui possède une paire de côtés parallèles, un parallélogramme.

Résumons maintenant ces deux propriétés :