Relation de Chasles

Dans cette vidéo, nous allons aborder la relation de Chasles. La relation de Chasles nous explique la règle d'addition pour les vecteurs.

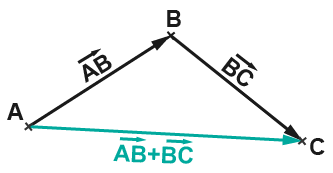
La relation de Chasles s'applique là où le point d'arrivée et le point de départ des vecteurs qu'on additionne coïncident, par exemple $\overrightarrow{A\textcolor{green}{B}} + \overrightarrow{\textcolor{green}{B}C}$ nous donnent $\overrightarrow{AC}$. On peut appliquer la relation de Chasles à une addition d'autant de vecteurs qu'on veut, pourvu que le point d'arrivée coïncide avec le point de départ du vecteur suivant. Par exemple $\overrightarrow{A\textcolor{green}{B}} + \overrightarrow{\textcolor{green}{B}\textcolor{red}C}+\overrightarrow{\textcolor{red}{C}D} = \overrightarrow{AD}$.

Il est important de comprendre que les vecteurs sont des translations. Donc tant que le point de départ et d'arrivée sont les mêmes, les vecteurs qui les représentent sont tous égaux. Comme on peut le voir ci dessus, qu'on fasse le chemin $\overrightarrow{AB} + \overrightarrow{BC}$, ou $\overrightarrow{AC}$, le point de départ est $A$, et le point d'arrivée est $C$. Ces deux translations nous amènent de $A$ à $C$ et sont donc égales.

On se sert de cette propriété pour arranger les termes dans le bon ordre, et ainsi voir plus facilement où on peut appliquer la relation de Chasles.

Voyons comment on peut utiliser la relation de Chasles pour simplifier une équation vectorielle. On sait déjà que $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$. On peut généraliser ceci : dès que la même lettre apparaît côte à côte, comme ici $B$, on peut la supprimer et réécrire le vecteur résultant comme ceci $\overrightarrow{A\cancel{B}} + \overrightarrow{\cancel{B}C} = \overrightarrow{AC}$.

Reprenons l'exemple ci-dessus et simplifions le :

On peut aussi faire l'opération inverse: ajouter des vecteurs tant que le point de départ et d'arrivée restent inchangés.

On voit qu'on peut ajouter autant de termes, ou de détours qu'on voudra, pourvu qu'on parte et qu'on arrive au même endroit.

Pour vérifier qu'on a pas fait d'erreurs, l'expression doit pouvoir se simplifier jusqu'au vecteur départ-arrivée, ici $\overrightarrow{AC}$. On a bien $\overrightarrow{AC} = \overrightarrow{A\cancel{B}} + \overrightarrow{\cancel{B}D} + \overrightarrow{DC} =\overrightarrow{A\cancel{D}}+ \overrightarrow{\cancel{D}C} =\overrightarrow{AC}$, donc le développement est correct.