Stabilité des allèles dans une population : Hardy-Weinberg

Sommaire

Génétique des populations

Modèle de Hardy-Weinberg

Exemple du modèle avec des allèles codominants

Détermination des fréquences alléliques mesurées dans une population

Détermination des fréquences de formation des différentes combinaisons génotypiques des couples possibles dans une population

Détermination de la probabilité d’apparition des différents génotypes pour chaque combinaison de couple

Constitution d'un tableau récapitulatif des différents génotypes pour chaque combinaison de couple

L'équilibre de Hardy Weinberg

Application du modèle pour les maladies autosomales récessives

Exemple de la phénylcétonurie

Pendant l’évolution biologique, la composition génétique des populations d’une espèce change de génération en génération.

Le modèle mathématique de Hardy-Weinberg, utilise la théorie des probabilités pour décrire le phénomène aléatoire de transmission des allèles dans une population. En assimilant les probabilités à des fréquences de taille (loi des grands nombres) le modèle prédit que la structure génétique d’une population de grand effectif est stable d’une génération à une autre sous certaines conditions. Cette stabilité est connue sous le nom d’équilibre de Hardy-Weinberg.

Les écarts entre les fréquences observées dans les populations naturelles et les résultats du modèle s’expliquent notamment par les effets des forces évolutives.

Enonciation du modèle

La génétique des populations a pour objectif l’étude de la fréquence des gènes et des génotypes, et des facteurs susceptibles de modifier ces fréquences au cours des générations successives.

La loi de Hardy-Weinberg décrit les relations entre les fréquences génotypiques et les fréquences alléliques. Elle permet par exemple l’estimation de la fréquence des hétérozygotes pour les maladies récessives autosomiques.

Proposée indépendamment en 1908 par le mathématicien anglais Hardy (1877-1947) et le médecin allemand Weinberg (1862-1937), la loi de Hardy-Weinberg se définit ainsi:

Propriété

Dans une population les fréquences alléliques restent stables d’une génération à l’autre dans les conditions suivantes :

Condition n°1 : les unions se font au hasard (PANMIXIE)
Condition n°2 : l’effectif est infini (Loi des grands nombres)
Condition n°3 : le taux de mutations est de zéro
Condition n°4 : il n’y a pas de sélection gamétique, c'est-à-dire que pour un gène existant sous la forme de 2 allèles, il y a autant de gamètes de chaque sorte (PANGAMIE)
Condition n°5 : il n’y a pas de sélection zygotique, tous les génotypes sont censés avoir la même espérance de vie pour le gène considéré
Condition n°6 : les individus sont pareillement viables et fertiles, c'est-à-dire que la population est isolée, il n’y a ni migration, ni sélection contre un phénotype particulier, ni introduction d’individus extérieurs.
Conditions n°7 : les générations ne se chevauchent pas.

C’est un modèle car les conditions requises pour atteindre cet équilibre ne sont jamais atteintes dans la nature.

<b>Godfrey Harold Hardy 1877-1947</b><div><i>Godfrey Harold Hardy 1.jpg, Auteur inconnu, via Wikimédia Commons, domaine publique, https://commons.wikimedia.org/wiki/File:Godfrey_Harold_Hardy_1.jpg</i><b><br></b></div> — **Godfrey Harold Hardy 1877-1947**
*Godfrey Harold Hardy 1.jpg, Auteur inconnu, via Wikimédia Commons, domaine publique, https://commons.wikimedia.org/wiki/File:Godfrey_Harold_Hardy_1.jpg*

Démonstration du modèle

L’objectif est de déterminer si dans une population, les fréquences des différents génotypes et donc les fréquences alléliques perdurent dans le temps. En d’autres termes, on doit vérifier qu’à chaque génération les fréquences alléliques restent les mêmes.

Exemple

Prenons l’exemple d’un locus qui peut être occupé par deux allèles A et a.

L’estimation de la fréquence des gènes à partir des génotypes n’est possible que si tous les génotypes sont identifiables : les deux allèles sont codominants. Il est tout de même possible de travailler avec des allèles dont l’un domine l’autre. Il suffira de procéder à une analyse génétique de la population pour connaître le nombre d’individus de chaque génotype.

Dans tous les cas avec 2 allèles, il est possible de produire trois génotypes : (A//A), (A//a) et (a//a)

Il va donc falloir déterminer les fréquences des allèles dans la population de départ considérée comme la génération 0. Cela nous permettra de déterminer la fréquence des différentes combinaisons de génotypes des différents couples formés dans cette même population. On pourra alors en déduire la probabilité d’apparition des différents génotypes chez leurs descendants et retrouver les fréquences théoriques des allèles dans cette génération 1.

Si les fréquences théoriques des allèles dans la génération 1 est égale à celles de la génération 0 alors le modèle de Hardy-Weinberg est valide.

Détermination des fréquences alléliques mesurées dans une population

Nommons u la fréquence mesurée du génotype homozygote dominant (A//A)
Nommons v la fréquence mesurée du génotype hétérozygote (A//a)
Nommons w la fréquence mesurée du génotype homozygote récessif (a//a)

La somme de ces fréquences (u + v + w) donne 1.

La fréquence de l’allèle A dans la population, est nommée p. Déterminons la formule nous permettant de trouver p à partir des fréquences mesurées des génotypes.

On sait que l’allèle « A » est retrouvé à la fois chez les homozygotes dominants et chez les hétérozygotes. Il y a donc 2 exemplaires de l’allèle A chez l’homozygote et 1 seul exemplaire chez l’hétérozygote. Ainsi la fréquence de l’allèle « A » correspond à la somme de la fréquence de cet allèle « A » dans les différents génotypes de la population :

u/2 + u/2 chez l’homozygote
v/2 chez l’hétérozygote

Soit au total :

p = \frac{u}{2}+\frac{u}{2}+ \frac{v}{2} = u+\frac{v}{2}

La fréquence de l’allèle « a » dans la population est nommée q (q est en général utilisé pour désigner l’allèle récessif). Or l’allèle « a » est retrouvé à la fois chez les homozygotes récessifs et chez les hétérozygotes. Ainsi la fréquence de l’allèle « a » correspond à la somme de la fréquence de cet allèle « a » dans les génotypes de la population, soit :

q = w+\frac{v}{2}

En additionnant p et q on retrouve :

u + \frac{v}{2} + w + \frac{v}{2} = u + v + w = 1

Exemple

Considérons une population de 10 individus et un gène donné avec deux allèles possibles A et a. Il y a donc au total 20 allèles dans ce groupe.

Supposons que les génotypes des individus soient les suivants :

(A//A), (A//a), (A//A), (a//a), (A//a), (A//A), (A//A), (A//a), (A//a), et (A//A)

Alors les fréquences alléliques p de l’allèle A et q de l’allèle a, avec p + q = 1, sont :

p = (2 +1 +2+0+1+2+2+1+1+2)\div20=0,7

et donc :

q = 1 - p = 0.3

Ou :

q = (0+1+0+2+1+0+0+1+1+0)\div20 = 0.3

Donc si on choisit un chromosome ou un gamète (ce qui revient au même) au hasard dans l'ensemble de cette population, il a 70 % de chance de porter l’allèle A et 30 % de chance de porter l'allèle a.

S'il y a plus de deux allèles différents, la fréquence de chaque allèle est simplement la fréquence de son homozygote plus la moitié de la somme des fréquences des hétérozygotes dans lesquels il apparaît.

Détermination des fréquences de formation des différentes combinaisons génotypiques des couples possibles dans une population

On considère que le gène étudié est autosomique et que donc la fréquence des allèles est identique pour chacun des deux sexes (ce qui ne serait pas le cas s'ils étaient portés par un chromosome sexuel).

On considère que les couples se forment au hasard (Panmixie), c’est la condition n°1 du modèle de Hardy-weinberg.

Pour pouvoir considérer que les fréquences des couples sont égales à leur probabilité, on considère que la population est de taille infinie pour pouvoir appliquer la loi des grands nombres. C’est la condition n°2 du modèle de Hardy-Weinberg.

Exemple

En effet, prenons l’exemple d’un lancer de dé. Lors de lancers d’un dé équilibré, les six faces n’apparaîtront pas aussi souvent les unes que les autres en pratique, mais la fréquence d’apparition de chaque face sera proche de sa probabilité d’apparition qui est de 1/6. Plus le nombre de lancers sera grand plus la fréquence approchera les 1/6.

Si je lance le dé 4 fois, la fréquence d’apparition d’au moins 2 faces sera forcément égale à 0. Si je le lance 40 fois j’ai plus de chance de voir apparaître toutes les faces et je pourrais déterminer une fréquence d’apparition pour chacune d’elle. Si je le lance 400 fois, j’aurais effectué suffisamment de lancers pour offrir à chaque face la possibilité d’apparaître autant de fois que les autres et la fréquence d’apparition aura donc tendance à s’approcher de 1/6.

Essayons de déterminer la fréquence de chacune des différentes combinaisons possibles de génotypes lors de la formation d’un couple. Pour cela nous allons réaliser un tableau de croisement des différents génotypes possibles pour chaque individu pris au hasard dans la population.

Propriété

Dans les titres des colonnes, on inscrit les génotypes possibles pour un individu et la fréquence de chacun. Dans les titres de lignes, on fait de même pour l’autre individu. Le croisement d’une ligne et d’une colonne correspond donc à un couple et la probabilité que les génotypes de ces 2 partenaires s’associent correspond à la combinaison de la fréquence de ces 2 génotypes.

<b>Tableau de croisement des unions possibles</b> — **Tableau de croisement des unions possibles**

La probabilité qu’un couple dont les 2 individus soient tous 2 de génotype (A//A) est donc de

u \times u= u^2

car chaque individu possède la probabilité u d'être (A//A).

Idem pour les autres associations de génotypes identiques.

Intéressons-nous maintenant aux probabilités de formation de couples aux génotypes différents

Ainsi les probabilités de former les couples sont :

u^2

Pour le couple (A//A) x (A//A)

v^2

Pour le couple (A//a) x (A//a)

w^2

Pour le couple (a//a) x (a//a)

uv + uv = 2 uv

Pour le couple (A//A) x (A//a)

uw + uw = 2 uw

Pour le couple (A//A) x (a//a)

vw + vw = 2 uw

Pour le couple (A//a) x (a//a)

Détermination de la probabilité d’apparition des différents génotypes pour chaque combinaison de couple

L’objectif est de déterminer si les fréquences des différents génotypes et donc les fréquences alléliques perdurent dans le temps. En d’autres termes on doit vérifier qu’à chaque génération les fréquences restent les mêmes.

On a travaillé à calculer la probabilité (et donc la fréquence puisqu’on travaille à grande échelle) de chaque combinaison de génotypes chez les couples.

On doit maintenant déterminer la fréquence possible des différents génotypes dans la génération 1. Pour cela il faut déterminer pour chacune des combinaisons possibles de couples, la probabilité d’apparition de chaque sorte de génotype dans leur descendance. On procèdera ensuite à la somme des probabilités obtenues pour obtenir la probabilité d’apparition c'est-à-dire la fréquence possible de chacun des génotypes dans la population de génération 1.

Déterminons donc pour chacun des couples possibles, la probabilité pour les enfants d’être de chacun des génotypes possibles à savoir (A//A) ou (A//a) ou (a//a).

Commençons par le couple (A//A) x (A//A) dont la probabilité de formation est de u2.

Chacun des 2 individus de ce couple ne peut produire qu’un seul type de gamète : (A/) Le tableau de croisement est donc le suivant :

Individu 1 Individu 2	(A/)
(A/)	(A//A)

Les enfants issus de ce couple ne peuvent donc présenter qu’un seul type de génotype : (A//A).

Ainsi dans ce couple la probabilité d’apparition du génotype (A//A) est de 1 et celle des génotypes (A//a) et (a//a) est de zéro chacune.

Si on élargit l’étude à la population, la probabilité d’apparition de ce génotype étant liée à la probabilité de la formation de ce couple, elle est donc au total de

1 \times u2 = u2

Celle des deux autres génotypes est donc de

0 \times u2 = 0

Continuons par le couple (a//a) x (a//a) dont la probabilité de formation est de w2.

Chacun des 2 individus de ce couple ne peut produire qu’un seul type de gamète : (a/) Le tableau de croisement est donc le suivant :

Individu 2 Individu 1	(a/)
(a/)	(a//a)

Les enfants issus de ce couple ne peuvent donc présenter qu’un seul type de génotype : (a//a).

Ainsi dans ce couple la probabilité d’apparition du génotype (a//a) est de 1 et celle des génotypes (A//A) et (A//a) est de zéro chacun.

Si on élargit l’étude à la population, la probabilité d’apparition de ce génotype étant liée à la probabilité de la formation de ce couple, elle est donc au total de :

1 \times w^2 = w^2

Celle des deux autres génotypes est donc de

0 \times w^2 = 0

Continuons pour le couple (A//a) x (A//a) dont la probabilité de formation est de v2.

Dans ce couple, chacun des individus produit 2 gamètes différents.

Le tableau de croisement est le suivant :

Individu 2 Individu 1	(A/)	(a/)
(A/)	(A//A)	(A//a)
(a/)	(A//a)	(a//a)

Les enfants issus de ce couple peuvent donc présenter 3 types de génotype (A//A), (A//a) et (a//a). Dans ce couple la probabilité d’apparition du génotype (A//A) est de 1/4, celle du génotype (A//a) est de 2/4 soit 1/2 et celle du génotype (a//a) est donc de 1/4.

Si on élargit l’étude à la population, les probabilités d’apparition de ces génotypes étant liées aux probabilités de la formation de ces couples, elles sont donc au total :

\frac{1}{4} \times v^2 = \frac{v^2}{4}

Pour (A//A)

\frac{1}{2} \times v^2 = \frac{v^2}{2}

Pour (A//a)

\frac{1}{4} \times v^2 = \frac{v^2}{4}

Pour (a//a)

Pour le couple (A//A) x (A//a) dont la probabilité de formation est de 2uv

Dans ce couple, un individu produit un seul type de gamète alors que l’autre en produit 2.

Le tableau de croisement est le suivant :

Individu 2 Individu 1	(A/)	(a/)
(A/)	(A//A)	(A//a)

Les enfants issus de ce couple peuvent donc présenter 2 types de génotype (A//A) et (A//a) en proportions équivalentes.

Ainsi dans ce couple la probabilité d’apparition du génotype (A//A) est de ½, celle du génotype (A//a) est de ½ et celle du génotype (a//a) est donc de zéro.

Si on élargit l’étude à la population, les probabilités d’apparition de ces génotypes étant liées aux probabilités de la formation de ces couples, elles sont donc au total :

\frac{1}{2} \times 2uv = uv

Pour (A//A)

\frac{1}{2} \times 2uv = uv

Pour (A//a)

0

Pour (a//a)

Pour le couple (A//A) x (a//a) dont la probabilité de formation est de 2uw.

Dans ce couple, chaque individu ne produit qu’un seul type de gamète.

Le tableau de croisement est le suivant :

Individu 2 Individu 1	(a/)
(A/)	(A//a)
(a/)	(a//a)

Les enfants issus de ce couple peuvent donc présenter 2 types de génotype (A//a) et (a//a).

Dans ce couple la probabilité d’apparition du génotype (A//a) est de 1/2 et celle du génotype (a//a) est de ½. Celle de (A//A) est de 0.

Si on élargit l’étude à la population, les probabilités d’apparition de ces génotypes étant liées aux probabilités de la formation de ces couples, elles sont donc au total :

\frac{1}{2} \times 2vw = vw

Pour (A//a)

\frac{1}{2} \times 2vw = vw

Pour (a//a)

0

Pour (A//A)

Si on récapitule tout cela dans un tableau et que l’on procède aux additions, on va pouvoir obtenir la probabilité d’apparition de chaque génotype dans la génération 1 issue de la génération 0 des parents :

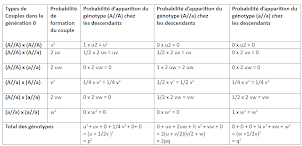
Conclusion

Ainsi dans une population la probabilité de trouver en génération 1 :

le génotype (A//A) est de :

p^2

le génotype (A//a) est de :

2pq

le génotype (a//a) est de :

q^2

La somme de toutes ces probabilités d’apparition des différents génotypes donne :

p^2 +2pq + q^2

et elle égale à 1 (100%).

De manière simplifiée, en traçant le tableau de croisement théorique des 2 allèles présents dans la génération 0 d’une population, on obtient 3 génotypes en génération 1 dans les proportions suivantes :

Individu 2 Individu 1	Fréquence de l’allèle A p	Fréquence de l’allèle a q
Fréquence de l’allèle A p	$p^2$	pq
Fréquence de l’allèle a q	pq	$q^2$

La somme des probabilités d’apparition des différents génotypes possibles dans la génération 1 est égale à 1 soit :

p^2 +2pq + q^2 = 1

Détermination de la probabilité d’apparition des allèles dans la génération 1

À partir de ce modèle on peut tirer la fréquence théorique d’apparition d’un allèle dans la génération 1.

Fréquence théorique de l’allèle A :

On utilise le même raisonnement que pour déterminer la fréquence mesurée des allèles. Dans le tableau théorique, l’allèle A est présent dans les génotypes (A//A) et (A//a). Ainsi sa fréquence théorique est équivalente à :

(p^2 + \frac{1}{2} \times 2pq) = p^2 + pq = p(p + q)

p + q =1

donc elle est égale à p.

Fréquence théorique de l’allèle a :

Dans le tableau théorique, l’allèle a est présent dans les génotypes (a//a) et (A//a). Ainsi sa fréquence théorique est équivalente à

(q^2 +\frac{1}{2}\times 2pq) = q^2 + pq = q(q + p)

p + q =1

donc elle est égale à q.

On constate ici que la fréquence théorique des différents allèles dans la génération 1 est égale à leur fréquence mesurée dans la génération 0.

Le modèle de Hardy-Weinberg permet bien de conclure que la population est stable et maintient son polymorphisme génétique en l’état si les conditions sont respectées.

Ainsi donc les fréquences génotypiques et alléliques d’un gène autosomique sont rigoureusement invariants d’une génération à une autre.

Application du modèle pour les maladies autosomales récessives

Si les hétérozygotes ne sont pas reconnaissables (dominance complète d’un allèle), dans l’hypothèse où les génotypes sont en équilibre, les fréquences alléliques et les fréquences de génotypes peuvent être estimées si la fréquence de l’homozygote rare est connue.

Proposition

Supposons une maladie récessive liée à des mutations homozygotes d’un gène biallélique, A représentant l’allèle normal et a l’allèle muté.

Le phénotype des individus présentant les génotypes (A//A) et (A//a) est identique.

Par contre, la probabilité d’apparition d’individus (a//a) correspond à :

q^2

On peut donc en déduire

q=\sqrt{q^2}

p= 1-q

La fréquence d’apparition des hétérozygotes (A//a) correspond à 2pq et peut être calculée :

2pq = 2 \times \sqrt{q^2} \times (1- \sqrt{q^2})

Si q est très petit,

1 - \sqrt{q^2}

est très proche de 1, donc

2pq \approx2\sqrt{q^2}

Exemple

La phénylcétonurie est une maladie récessive autosomique qui atteint un enfant sur 10 000.

q = \sqrt{1} \div 10 000 = \frac{1}{10000}

2 pq = 2 \times \frac{1}{100} \times (1 – \frac{1}{100})

1 – \frac{1}{100} = \frac{99}{100}

très peu différent de 1, donc :

2pq \approx 2\times \frac{1}{100} \approx \frac{1}{50}

Ainsi dans la population, un individu pris au hasard a un risque sur 50 d’être hétérozygote.

Voilà comment à partir du nombre d’individus homozygotes récessifs comptabilisés, on arrive grâce au modèle de Hardy Weinberg, à déterminer le risque pour un individu pris au hasard dans une population d’être hétérozygote pour une maladie génétique.

Revenir au chapitre

Cours

Exercices

Stabilité des allèles dans une population : Hardy-Weinberg

Enonciation du modèle

Propriété

Démonstration du modèle

Exemple

Détermination des fréquences alléliques mesurées dans une population

Exemple

Détermination des fréquences de formation des différentes combinaisons génotypiques des couples possibles dans une population

Exemple

Propriété

Détermination de la probabilité d’apparition des différents génotypes pour chaque combinaison de couple

Conclusion

Détermination de la probabilité d’apparition des allèles dans la génération 1

Application du modèle pour les maladies autosomales récessives

Proposition

Exemple

Classes

Entreprise

Réseaux sociaux