


La fonction exponentielle
Fonction exponentielle
Définition et propriétés générales
Définition
La fonction exponentielle notée est la seule fonction vérifiant :
est dérivable sur
.

La nombre est aussi noté .
Propriété
La fonction exponentielle est :
définie sur
continue
strictement positive
strictement croissante.
Propriété
L'image de par la fonction est notée . Donc .
Propriété
Pour tout réels et , pour tout entier ,

Attention : .
Représentation graphique de la fonction exponentielle
La courbe de la fonction exponentielle est continue et se dessine toujours au dessus de l'axe des abscisses : est définie sur et .
Elle "touche" presque l'axe des abscisses en : .
La courbe croît de plus en plus vite vers : .
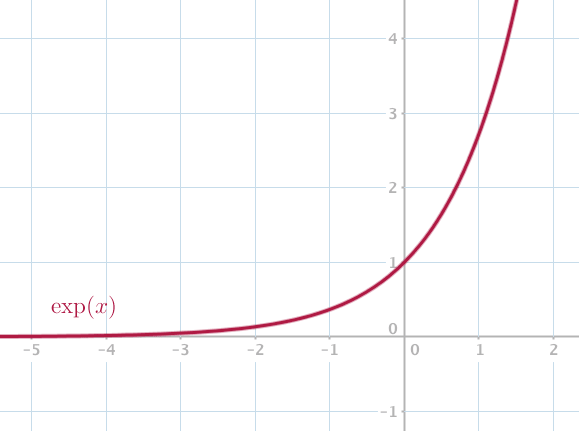
Courbe de la fonction exponentielle
Etude de la fonction exponentielle : équations, inéquations, limites et dérivée
Équations et Inéquations avec la fonction exponentielle
Propriété
Pour tout réels et ,
.

Ces propriétés sont vrais car la fonction est strictement croissante
Limites de la fonction exponentielle
Propriété
Propriété
Pour tout entier naturel ,

Ces propriétés sont vrais car la fonction croît plus vite que les fonctions polynomiales
Dérivée de la fonction exponentielle
Propriété
Pour tout réel , .
Propriété
Pour toute fonction , .

Remarquons que comme , le signe de la dérivée ne dépend que de , Les variations de sont les mêmes que la fonction .

Mots clés à retenir : Exponentielle, Croissante, Positive.
Commentaires
Knight M.RZ
0
Dommage qu'il n'y ait pas les démonstrations des limites de référence références





