


Forces et Lois de Newton
Les lois de Newton
Référentiels galiléens
Définition
Pour simplifier l’étude d’un mouvement, on choisit un référentiel adapté. Un référentiel dans lequel les lois de Newton sont vérifiées est un référentiel galiléen.
Exemple
un référentiel terrestre pour l’étude de mouvements de courte durée au voisinage de la Terre
le référentiel géocentrique pour l’étude du mouvement des satellites terrestres
le référentiel héliocentrique pour l’étude du mouvement des planètes dans le système solaire
Première loi
Remarque
Contrairement à ce que pensait Aristote, une force n’est pas nécessaire pour entretenir un mouvement. Galilée l’avait pressenti sans le prouver près de ans avant l’énoncé des lois par Newton.
Théorème
Dans un référentiel galiléen, si un système assimilé à un point matériel n’est soumis à aucune force (système isolé) ou s’il est soumis à un ensemble de forces qui se compensent (système pseudo-isolé), alors il est immobile ou animé d’un mouvement rectiligne uniforme.
Propriété
Lorsqu’un système est isolé ou pseudo-isolé, sa vitesse est constante donc sa quantité de mouvement se conserve.
Deuxième loi
Théorème
Dans un référentiel galiléen, si un système assimilé à un point matériel est soumis à une ou plusieurs forces extérieures, alors la somme vectorielle de ces forces notée est égale à la dérivée par rapport au temps de son vecteur quantité de mouvement :
Propriété
Si le système conserve une masse constante au cours du temps, cette loi peut alors s’écrire :
Troisième loi
Théorème
Si un système exerce sur un système une force alors le système exerce également sur le système une force . Ces deux forces ont même direction, même valeurs et sont de sens opposés. On écrit alors :

Attention, ces deux forces ne s’exercent pas sur le même système, lorsqu’on utilisera la deuxième loi de Newton, il ne faudra tenir compte que des forces extérieures au système (soit si le système considéré est ).
Exemple
Pour se déplacer, le piéton appuie sur le sol, le nageur sur l’eau, la fusée est propulsée par l’action du gaz éjecté.
Mouvement d’un système dans un champ uniforme
Cas d’un objet dans un champ de pesanteur uniforme
Système, choix du référentiel :
Toute étude de mouvement nécessite de définir le système et de choisir un référentiel adapté
Exemple
Dans le cas du lancer de la balle de masse :
système étudié : la balle
référentiel : terrestre
On fera l’étude dans le repère orthonormé avec une vitesse dans le plan vertical.
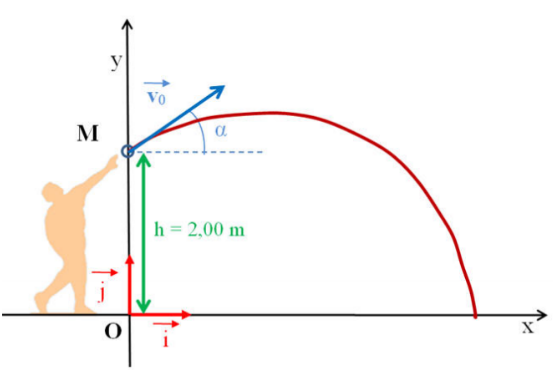
Schéma d'un lancer de balle.
Deuxième loi de Newton et accélération :
Exemple
Avant d’appliquer la deuxième loi de Newton, il faut faire l’inventaire des forces extérieures. Les forces extérieures exercées ici sur le point sont :
le poids de la balle
les forces exercées par l’air .
On négligera les forces de frottements dues à l’air car elles sont très faibles par rapport au poids.
Exemple
La masse ne variant pas au cours du temps, on a alors :
Or la seule force ici est le poids donc :
donc
On projette sur les axes sachant que est orienté selon vers le bas :
Vitesse :
Propriété
Le vecteur accélération est la dérivée du vecteur vitesse par rapport au temps
Exemple
Donc
Pour trouver le vecteur vitesse, on recherche la primitive par rapport au temps de chaque coordonnée du vecteur accélération, soit :
Pour trouver les valeurs des constantes , et on regarde les conditions initiales pour la vitesse soit :
Ce qui donne donc pour les coordonnées du vecteur :
Remarque
Comme est nulle, on aura alors un mouvement plan.
Position :
Propriété
Le vecteur vitesse est la dérivée par rapport au temps du vecteur position :
Exemple
Donc
On retrouve alors les coordonnées du vecteur en cherchant les primitives par rapport au temps des coordonnées du vecteur vitesse soit :
Les constantes , et sont trouvées grâce aux conditions initiales du vecteur position, on a alors :
Les coordonnées de et dépendent du temps, elles sont les équations horaires du mouvement.
Trajectoire :
Exemple
La trajectoire est l’ensemble des positions occupées par le point lors du mouvement. Cela revient à déterminer en fonction de dans ce cas de mouvement plan.
On a :
On peut donc écrire
On substitue dans l’équation donnant et on obtient :
L’équation est une fonction polynôme du second degré, ce qui signifie que la trajectoire est une parabole dont on peut trouver mathématiquement le maximum et les racines.
Généralités
Système, choix du référentiel :

On définit le système étudié, on choisit un référentiel et on fixe un repère.
Deuxième loi de Newton et accélération :

On établit un bilan des forces extérieures s’appliquant au système en négligeant, le plus souvent, les frottements.
A partir de la deuxième loi de Newton et du fait que la masse ne varie pas, on obtient une égalité pour le vecteur accélération.
Puis on projette le vecteur accélération sur le repère afin d’obtenir ses trois coordonnées.
Vitesse :

La vitesse est la dérivée de l’accélération par rapport au temps.
On recherche les primitives des coordonnées de par rapport au temps afin d’obtenir les coordonnées de la vitesse en fonction du temps.
On regarde ensuite les conditions initiales de la vitesse pour mettre des valeurs sur les constantes trouvées pour les coordonnées de la vitesse.
Position :

Le vecteur vitesse est la dérivée du vecteur position par rapport au temps.
On recherche les primitives des coordonnées de la vitesse par rapport au temps afin d’obtenir les coordonnées du vecteur position en fonction du temps.
On regarde ensuite les conditions initiales du vecteur position pour mettre des valeurs sur les constantes trouvées pour les coordonnées du vecteur position.
Les équations obtenues sont les équations horaires du mouvement.
Trajectoire :

Pour déterminer la trajectoire, on exprime en fonction de , pour cela :
on exprime en fonction de à partir de l’équation horaire
on substitue dans
L’équation de la trajectoire est le plus souvent un polynôme du second degré. Par résolution mathématique, on peut trouver :
la flèche ; la hauteur maximale atteinte par la balle
la portée ; la valeur de pour laquelle la balle touche le sol
Mouvement des satellites et planètes
Exemple
On étudie le mouvement d’un satellite de masse , assimilé à un point matériel, en orbite autour de la Terre de centre et de masse .
On se place dans l’approximation d’une orbite circulaire de rayon .
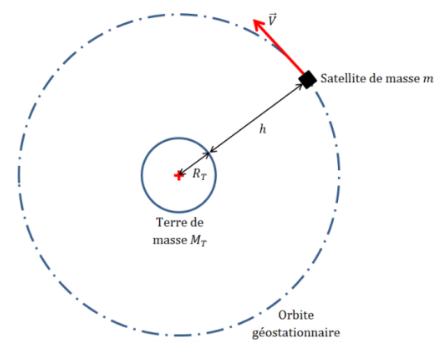
Mouvement d'un satellite en orbite.
Système étudié : le satellite
Référentiel choisi : référentiel géocentrique, considéré galiléen
Le mouvement est plan, on utilise un repère mobile lié au satellite et dont les axes sont dans le plan du mouvement. Dans le cas de l’étude, on considère que le satellite n’est soumis qu’à la force d’attraction gravitationnelle de la Terre (l’attraction des autres astres et les frottements de l’atmosphère sont très négligeables). Selon la deuxième loi de Newton on a :
Or ainsi donc : Le vecteur accélération est centripète, dirigé vers le centre de la trajectoire. Comme vu au chapitre sur la cinématique :
avec et . étant la valeur de la vitesse. On en déduit logiquement que :
Comme alors est constante, le mouvement est circulaire uniforme. Et
La valeur de la vitesse du satellite est indépendante de sa masse mais dépendra de , et donc de son altitude. Elle diminue lorsqu’elle augmente. La durée pour faire un tour est la période de révolution. Elle est égale au périmètre de la trajectoire divisé par la valeur de la vitesse pour un mouvement uniforme.
La période de révolution, comme la vitesse, du satellite est indépendante de sa masse mais dépend du rayon de la trajectoire et donc de l’altitude. Elle augmente lorsque celle-ci augmente.
Remarque
Cette étude peut être généralisée à tout satellite en orbite circulaire autour de la Terre.
Dans l’approximation des trajectoires circulaires, l’application de la deuxième loi de Newton à l’étude du mouvement d’un satellite d’une planète permet de montrer que le mouvement est uniforme et d’établir l’expression de la valeur de sa vitesse et de sa période de révolution.
Commentaires
Amira
0
Salut, peut-on imprimer un cour??
lilou
0
salut je n'arrive toujours pas a comprendre la méthode pour faire une étude de mouvement
mattoche
0
salut
RAB78
0
comment trouver les équation d'une MRU et MRUV
RAB78
0
comment faire pour trouver l'équation
d'une MRU et MRUV





