Limites de fonctions

Définitions

Limite finie et infinie lorsque x tend vers l'infini

Définition

Soit $f$ une fonction définie au moins sur un intervalle de $\mathbb{R}$ du type $]a ; +\infty[$ . La fonction $f$ a pour limite $l$ en $+\infty$ si tout intervalle ouvert contenant $l$ contient toutes les valeurs de $f(x)$ pour $x$ assez grand.

On note alors $\lim\limits_{x \to \infty} f(x) = l$ .

Propriété

La droite d’équation $y = l$ est asymptote horizontale à $C_f$ en $+\infty$ si $\lim\limits_{x \to \infty} f(x) = l$ .

Définition

La fonction $f$ a pour limite $+\infty$ en $+\infty$ si tout intervalle de $\mathbb{R}$ du type $]a ; +\infty[$ contient toutes les valeurs de $f(x)$ pour $x$ assez grand. On note alors : $\lim\limits_{x \to \infty} f(x) = +\infty$ .

Limite infinie lorsque x tend vers un réel a

Définition

Soit $f$ une fonction définie sur un intervalle ouvert de $\mathbb{R}$ du type $]a - \epsilon ; a[$ ou $]a ; a + \epsilon[$ . La fonction $f$ a pour limite $+\infty$ en $a$ si tout intervalle de $\mathbb{R}$ du type $]A ; +\infty[$ contient toutes les valeurs de $f(x)$ pour $x$ assez proche de $a$ . On note alors : $\lim\limits_{x \to a} f(x) = +\infty$ .

Propriété

La droite d’équation $x = a$ est asymptote verticale à $C_f$ si $\lim\limits_{x \to a} f(x) = +\infty$ .

Opérations sur les limites

Limite d'une somme

Propriété

si $f$ ou $u_{n}$ a pour limite	$c$	$c$	$c$	$+ \infty$	$-\infty$	$+\infty$
si $g$ ou $v_{n}$ a pour limite	$c'$	$+\infty$	$-\infty$	$+\infty$	$-\infty$	$-\infty$
alors $f+g$ ou $(u_{n})+(v_{n})$ a pour limite	$c+c'$	$+\infty$	$-\infty$	$+\infty$	$-\infty$	pas de résultat général

Limite d'un produit

Propriété

si $f$ ou $u_{n}$ a pour limite	$c$	$c \neq 0$	$+ \infty$ ou $-\infty$	$0$
si $g$ ou $v_{n}$ a pour limite	$c'$	$+\infty$ ou $-\infty$	$+\infty$ ou $-\infty$	$+\infty$ ou $-\infty$
alors $f \times g$ ou $(u_{n}) \times (v_{n})$ a pour limite	$c \times c'$	$+\infty$ ou $-\infty$ suivant les signes	$+\infty$ ou $-\infty$ suivant les signes	pas de résultat général

Limite d'un inverse

Théorème

si $f$ ou $u_{n}$ a pour limite	$c \neq 0$	$0^-$	$0^+$	$+ \infty$ ou $-\infty$
alors $\dfrac{1}{f}$ ou $\dfrac{1}{u_{n}}$ a pour limite	$\dfrac{1}{c}$	$-\infty$	$+\infty$	$0$

Limite d'un quotient

Propriété

si $f$ ou $u_{n}$ a pour limite	$c$	$c$	$c \neq 0$	$0$	$+\infty$ ou $-\infty$	$+\infty$ ou $-\infty$	$+\infty$ ou $-\infty$
si $g$ ou $v_{n}$ a pour limite	$c' \neq 0$	$+\infty$ ou $-\infty$	$0$	$0$	$0$	$c' \neq 0$	$+\infty$ ou $-\infty$
alors $\dfrac{f}{g}$ ou $\dfrac{u_{n}}{v_{n}}$ a pour limite	$\dfrac{c}{c'}$	$0$	$+\infty$ ou $-\infty$ suivant les signes	pas de résultat général	$+\infty$ ou $-\infty$ suivant les signes	$+\infty$ ou $-\infty$ suivant les signes	pas de résultat général

Les formes indéterminées

Propriété

On dit qu'il y a forme indéterminée lorsqu'on ne peut pas trouver une limite en utilisant les tableaux précédents.

Pour trouver la limite en cas de forme indéterminée on effectue les manipulations suivantes :

$\frac{∞}{∞}$ : Factorisation des termes "dominants" puis simplification.
$\frac{0}{0}$ : Factorisation d'un terme tendant vers $0$ puis simplification.

Attention : Ne jamais rédiger en devoir les notations $+\infty - \infty$ et $\frac{\infty}{ \infty}$ ...

Limites et inégalités

Dans ce qui suit, $I$ désigne un intervalle.

Limites par comparaison

Propriété

Si pour tout $x \in I :$ $f(x) \geq g(x)$ et si $\lim g(x) = + \infty$ alors $\lim f(x) = + \infty$
Si pour tout $x \in I :$ $|f(x)-c|\leq g(x)$ et si $\lim g(x) = 0$ alors $\lim f(x) = c$

Comparaison de limites

Propriété

Si pour tout $x \in I :$ $f(x)\leq g(x)$ , si $\lim f(x) = c$ et $\lim g(x) = c'$ alors $c \leq c'$

Théorèmedes gendarmes ou théorème d'encadrement

Si pour tout $x \in I$ : $f(x)\leq g(x) \leq h(x)$ et $\lim f(x) =\lim h(x)= c$ alors $\lim f(x) = c$

Droites parallèles à un axe de coordonnées asymptotes à une courbe

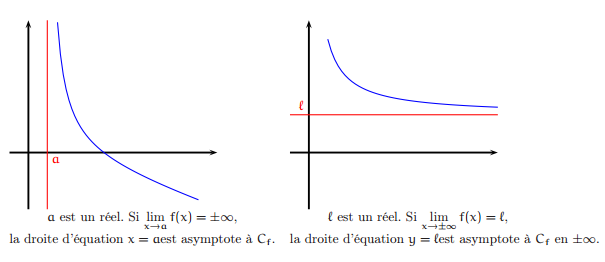
Figure expliquant comment dessiner les droites parallèles à un axe de coordonnées asymptotes à une courbe.

Mots clés à retenir : Limite, Forme indéterminée, Gendarmes ou encadrement.

Limites de fonctions

Définitions

Limite finie et infinie lorsque x tend vers l'infini

Définition

Propriété

Définition

Limite infinie lorsque x tend vers un réel a

Définition

Propriété

Opérations sur les limites

Limite d'une somme

Propriété

Limite d'un produit

Propriété

Limite d'un inverse

Théorème

Limite d'un quotient

Propriété

Les formes indéterminées

Propriété

Limites et inégalités

Limites par comparaison

Propriété

Comparaison de limites

Propriété

Théorèmedes gendarmes ou théorème d'encadrement

Droites parallèles à un axe de coordonnées asymptotes à une courbe

rida-khiat

valentine8890

manon_fl31

Axellito

Yona

Yona

a.abdelillah

a.abdelillah

VITHUU

VITHUU

Classes

Entreprise

Réseaux sociaux