S'abonner
TerminaleMathématiquesPrimitives et équations différentielles
decoration
decorationdecoration

Primitives

Généralités sur les primitives

Interprétation graphique

Si ff est une fonction continue et positive sur un intervalle [a,b][a,b] et (C)(C) sa courbe dans un repère orthogonal. l'intégrale est le réel mesurant l'aire, en unités d'aire, de la partie du plan limitée par la courbe (C)(C), l'axe des abscisses et les droites d'équations x=ax=a et x=bx=b.

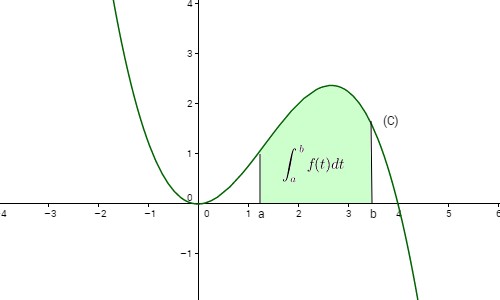
Interprétation graphique de l'intégrale

Interprétation graphique de l'intégrale

Définition et propriétés générales

Définition

Soit ff une fonction définie sur un intervalle II. On appelle primitive de la fonction ff sur l’intervalle II toute fonction FFdéfinie et dérivable sur II telle que F′=f.F' = f. On peut l'écrire comme suit :x↦F(x)=∫xf(t)dt.x\mapsto F(x) = \int^{x}f(t)dt.

Propriété

Toute fonction continue sur un intervalle II admet une primitive sur II.

lumix

La différence entre primitive et intégrale est qu'une primitive est une fonction tandis qu'une intégrale est un réel exprimé comme une aire algébrique (pouvant être négatif).

Propriété

Soit ff une fonction définie sur les intervalles considérés,

  • ∫aa​f(t)dt=0.

  • ∫ab​f(t)dt=−∫ba​f(t)dt.

  • ∫ab​f(t)dt=∫ac​f(t)dt+∫cb​f(t)dt.

  • Si k∈Rk \in \mathbb{R} alors ∫abkf(t)dt=k∫abf(t)dt.\displaystyle\int _{a} ^{b}kf(t)dt=k\int _{a} ^{b}f(t)dt.

Propriété

Soient ff et gg deux fonctions définies sur les intervalles considérés, Si a≤ba \leq b et si pour tout xx de [a,b][a,b] on a f(x)≥0,f(x) \geq 0, alors∫abf(x)dx≥0.\displaystyle\int_{a}^{b}f(x)dx \geq 0.

Si a≤ba \leq b et si pour tout xx de [a,b][a,b] on a f(x)≤g(x),f(x) \leq g(x), alors∫abf(x)dx≤∫abg(x)dx.\displaystyle\int_{a}^{b}f(x)dx \leq \int_{a}^{b}g(x)dx.

Compléments

Propriété

Soit ff une fonction définie sur les intervalles considérés,

  • Si ff est une fonction paire alors ∫−aaf(t)dt=2∫0af(t)dt.\displaystyle\int _{-a}^{a}f(t)dt=2\int _{0} ^{a}f(t)dt.

  • Si ff est une fonction impaire alors ∫−aaf(t)dt=0.\displaystyle\int _{-a}^{a}f(t)dt=0.

  • Si ff est une fonction impaire alors ∫−aaf(t)dt=0.\displaystyle\int _{-a}^{a}f(t)dt=0.

  • Si ff est une fonction périodique de période TT alors∫aa+Tf(t)dt=∫t0Tf(t)dt.\displaystyle\int_{a}^{a+T} f(t)dt= \int_{t_{0}}^{T}f(t)dt.

Définition

On appelle valeur moyenne de ff sur [a,b][a,b], le réel 1b−a∫abf(t)dt.\displaystyle\frac{1}{b-a} \int_{a}^{b}f(t)dt.

Théorèmede la valeur moyenne

S'il existe deux réels mm et MM tels que pour tout xx de [a,b][a,b] (a≤b)(a \leq b), m≤f(x)≤Mm \leq f(x) \leq M, alorsm(b−a)≤∫abf(t)dt≤M(b−a)m(b-a) \leq \displaystyle\int_{a}^{b} f(t) dt \leq M(b-a)

Primitives usuelles

Propriété

f(x)f(x)F(x)F(x)
00constante aa
xnx^nxn+1n+1\dfrac{x^{n+1}}{n+1}
exe^xexe^x
sin⁡(x)\sin(x)−cos⁡(x)-\cos(x)
cos⁡(x)\cos(x)sin⁡(x)\sin(x)
1x\dfrac{1}{x}ln⁡(x)\ln(x)
u′+v′u'+v'u+vu+v
u′v+uv′u'v+uv'uvuv
u′unu'u^nun+1n+1\dfrac{u^{n+1}}{n+1}
u′u\dfrac{u'}{u}ln⁡(u)\ln(u)
u′u\dfrac{u'}{\sqrt{u}}2u2\sqrt{u}
u′euu'e^{u}eue^u

lumix

Mots clés à retenir : Intégrale, Primitive, Chasles.

Commentaires
Inscris-toi en 30 secondes pour poser ta question !

Réseaux sociaux