


Dynamique
Aspect historique
La dynamique est la partie de la mécanique qui s’occupe des mouvements et des causes de ceux-ci. Cette science existe depuis l’antiquité, le premier ayant proposé un modèle étant le philosophe Aristote.

Représentation aristotélicienne : « La vitesse d’un corps dépend en module de la force qui lui est appliquée et a la même direction et le même sens ». Ainsi d’après lui si on n’applique pas de force sur un corps il ne bougera pas.

La théorie de l’impetus : Au cours des siècles qui ont suivi ce modèle n’a pas survécu. En effet l’expérience de tous les jours tend à démontrer son inexactitude, car si on lance quelque chose en l’air on ne lui applique pas de force et pourtant il continue à bouger. C’est dans cette faille qu’a pris forme la théorie de l’impetus : « Au début du lancé on applique au corps un certain impetus qui diminue au cours du mouvement. La vitesse de celui-ci dépend en module de l’impetus et a la même direction et le même sens. »
Loide Newton
La mécanique newtonienne : S’appuyant sur les travaux de l’astronome Kepler, le jeune Newton émit l’hypothèse que la mécanique céleste (le mouvement des étoiles) subissait les mêmes lois que la mécanique terrestre (ce qui se passe ici bas) et que cette mécanique est régit par lois :
Le centre d’inertie d’un corps qui isolé subit une résultante des actions mécaniques extérieures nulle est soit fixe, soit en mouvement de translation rectiligne à vitesse constante par rapport à un repère fixe (cette loi avait déjà été énoncée par Galilée comme le principe d’inertie).
L'accélération par rapport à un repère fixe (accélération Galiléenne) que subit un corps isolé est directement lié à la résultante des actions mécaniques extérieure.
Théorème de la résultante dynamique :Un corps subissant une action mécanique de la part d’un autre, applique sur cet autre une réaction de même intensité et direction mais de sens opposé. C’est le principe que vous maîtrisez déjà de l’action réaction.
L’application de ces lois d’énoncé très simple ont permis (et permettent toujours) de réaliser des prédictions d’une étonnante précision. L'engouement des scientifiques et mathématiciens fut tel que certain pensaient pouvoir à partir de ces seules lois décrire la totalité de l’univers physique et de pouvoir même aller jusqu'à prédire l’avenir. Ce fut l’ère déterministe.
Vous avez dit repère ?
Le problème dans les premières lois de Newton est quelles sont vraies par rapport à un repère fixe. Mais pour trouver concrètement un repère fixe on se heurte à de sordides problèmes matériels : Ne dit on pas que la terre tourne ? Ne dit on pas que l’espace est en expansion ?
On nomme repère Galiléen le repère fixe mais comme il est impossible de le trouver on fera certaines approximations en considérant par hypothèse qu’un repère fixe par rapport au sol de la terre est Galiléen.
Centre de gravité ou centre d’inertie ?
Le centre d’inertie est le point autour duquel la matière est répartie également. C’est dans le cas d’un corps constitué de matière homogène le barycentre au sens mathématique du terme.
Le centre de gravité est quant à lui le point ou s’applique la résultante des actions mécaniques de gravité. Et il se trouve que dans un champ de pesanteur homogène ces points sont coïncidents alors qu’en réalité il représentent bien choses totalement distincts.
Principe fondamentale de la dynamique généralisé
Propriété
Soit un ensemble de particules composant le solide à étudier . D’après la seconde loi de Newton on peut écrire :
Cette somme peut s’écrire sou la forme d’une intégrale avec A le point localisant chacune des particules :
Qui dans le cas de la translation se réduit à l’expression à connaître par cœur :
Dans le cas de cette loi la masse est appelée masse inerte (où inertie). Pour ce qui est de la formule bien connue du poids on nomme la masse pesante. Bien que d’appellations différentes l’expérience montre que ces grandeurs sont équivalentes d’où l’utilisation généralisée du terme masse sans qualificatifs additionnels.
Que se passe t’il pour les autres mouvements ?
Le problème avec d’autres mouvements que celui de translation rectiligne est que les différentes particules de matière ne subissent pas les mêmes accélérations à tout instant. Les seuls cas autres que nous considéreront pré-bac seront simplement ceux de rotation autour d’un axe fixe centre principal d’inertie.
Propriété
Ces mouvements seront régit par la loi déduite de la seconde loi de Newton :
Et si on souhaite ne s’occuper que que mouvements autour d’un axe fixe principal d’inertie cela revient a remplacer les par . Avec
Ce qui en définitive se réduit à :
Théorèmedu moment dynamique
Avec :
le couple en N.m,
le moment principal en kg/m d’inertie
point l’accélération en rotation en rad/s
| Définition (kg) | Cylindre plein masse (kg) | Cylindre creux (couronne) masse (kg) | Sphère pleine masse (kg) |
|---|---|---|---|
| Rotation de rayon | Disque de rayon , rotation autour de l'axe du cylindre | Rayon intérieur et extérieur , rotation autour de l'axe du cylindre | Sphère de rayon , rotation autour d'un axe passant par le centre |
Détermination de lois horaires
En écrivant les équations de la dynamique pour un ensemble on peut facilement par intégrations successives prédire la position du système à tout instant.
Exemple
Exemple 1 : Un réacteur ionique de satellite produit sur lui une poussée de N. Ce dernier, de masse avoisinant la tonne, est lancé à une vitesse absolue de km/h dans le sens de la poussée au début de celle-ci.
Théorème de la résultante dynamique sur le satellite :
Ainsi on connaît la valeur de l’accélération Galiléenne : m/s.
On peut aussi connaître sa vitesse :
La constante d’intégration étant la vitesse initiale : .
Enfin on peut en déduire la position à tout instant par rapport à la position initiale :
Exemple
Exemple 2 : Vous essayez de pousser seul votre voiture qui ne veut pas démarrer. Elle pèse kg, vous fournissez un effort de N et elle oppose une résistance qui est fonction de la vitesse .
Théorème de la résultante dynamique sur la voiture :
Et comme accélération et vitesse sont liées :
Ce genre d’équation ce nomme équation différentielle nous n’aurons pas à les résoudre en pré-bac mais on s’aperçoit que pour une vitesse de 15 km/h l’accélération devient nulle ce qui veut dire que malgré le fait que vous fournissiez un effort il arrive un moment ou le solide n’accélère plus, ceci à cause de la résistance à l’avancement.
Résolution de problème
Principe fondamental de la dynamique (PFD)
Théorèmedu torseur dynamique
L’ensemble des actions mécaniques extérieures qui s’exercent sur un solide est égal au torseur dynamique.

Actions mécaniques extérieures : qui dit extérieures, dit intérieures et dit forcement frontière.
Traduction avec la modélisation vectorielle des actions mécaniques :
Propriété
Cas particulier : Si le système est sans mouvement, c'est-à-dire statique, alors :
La somme des forces extérieures exercées sur le système à l’équilibre est nulle.
La somme des moments des forces exercées sur le système à l’équilibre est nulle.
Utilité du PFD
La modélisation des actions mécaniques extérieures exercées sur un système conduit à distinguer éléments connus et éléments inconnus. Or la connaissance de ces inconnues peut être nécessaire pour :
Dimensionner des composants
Déterminer des déformations
Déterminer des risques de destruction des surfaces, etc…
Appliquer le PFD à un système pour lequel on connaît certaines actions mécaniques exercées sur celui-ci (données), permet de déterminer les actions mécaniques inconnues.
Il convient donc de recenser les actions (de contact ou à distance) extérieures au système isolé connues ou inconnues : c’est le BAME (Bilan des Actions Mécaniques Extérieures)
Traduction vectorielle du PFD
Sans mouvements, donc avec un torseur dynamique nul cela donne :
Théorèmede la résultante statique
est à l’équilibre par rapport au repère .
La résultante des actions mécaniques extérieures à est nulle. On note :
La somme des vecteurs modélisant les forces est égale au vecteur nul.
Théorèmedu moment résultant statique
est à l’équilibre par rapport à un repère .
Le moment résultant des actions extérieures à est nul. On note :
le point de réduction.
La somme des vecteurs modélisant les moments des forces extérieures à réduit au même point est égale au vecteur nul.
Remarque
Le système étant à l’équilibre, il ne peut pas être déformable car sinon les points d’application des actions ne resteront pas fixes, et donc il ne sera plus immobile.
Notion d’isostatisme et d’hyperstatisme
Définition
Le problème est isostatique si : L’application du PFS permet, à lui seul, de déterminer les inconnues.
Définition
Le problème est hyperstatique si : L’application du PFS ne permet pas, à lui seul, de déterminer les inconnues.
Remarque
Problème spatial : Le nombre maximum d’inconnues par isolement est de - nous ferons dans ces cas des résolutions assistées par ordinateur.
Problème plan : Le nombre maximum d’inconnues par isolement est de - dans ce cas nous procéderons a des résolutions analytiques.
Hypothèse de « problème plan »
Pour qu’un problème soit plan, il faut :
Un mécanisme plan : Les mouvements des pièces doivent avoir lieu dans un seul plan.
Une symétrie de chargement : On doit pouvoir représenter toutes les forces dans le plan de symétrie du mécanisme (les moments doivent être perpendiculaires à ce plan).
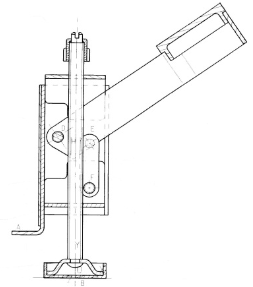
Mécanisme plan
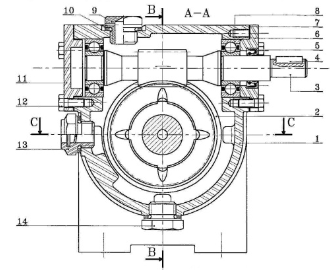
Mécanisme spatial
Cette hypothèse permet :
De diminuer le nombre d’équation à résoudre. Si le problème est plan alors les seules équations à développer sont :
- L’équation de la résultante selon l’axe
- L’équation de la résultante selon l’axe
- L’équation du moment selon l’axe
D’éviter de calculer certaines inconnues, car toutes ces inconnues seront nulles :
- Inconnues de la résultante selon l’axe
- Inconnues du moment selon l’axe
- Inconnues du moment selon l’axe
Ainsi il ne reste qu'une équation de moment, cette dernière se calcule en plusieurs étapes :
- S'imposer une convention de signe (prendre le sens + quad on tourne de l'axe vers ) :
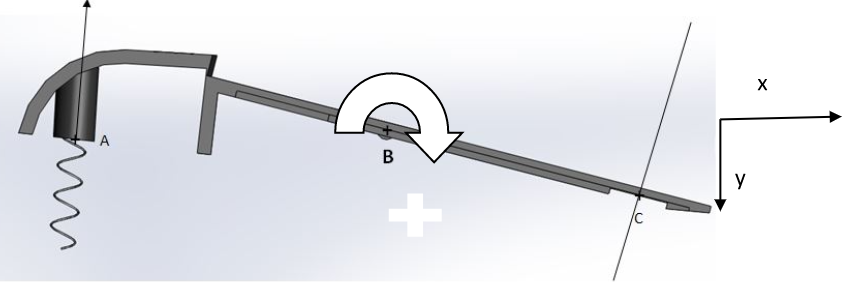
Solide en mouvement.
- Déterminer un centre de réduction des moments : prendre le point pour lequel vous ne connaissez pas de direction d'où qui à la plus d'inconnues :
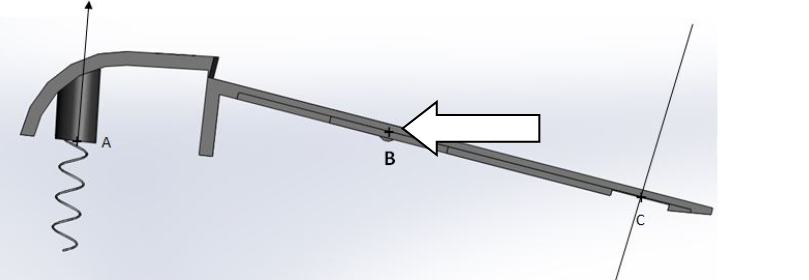
Solide en mouvement.
- Déterminer la valeur algébrique des moments exprimés dans ce centre.

Solide en mouvement.
Dans le cas ou le sens de l'action est inconnu, il faut s'en imposer un arbitrairement, en fin de résolution il sera confirmé ou infirmé

Solide en mouvement.
- Affecter les signes aux moments en fonction de la convention :
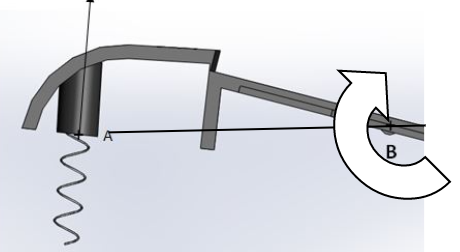
Solide en mouvement.
Pour ça il faut regarder le sens de rotation de la force autour du centre de réduction et le comparer à la convention de signe imposée au départ :
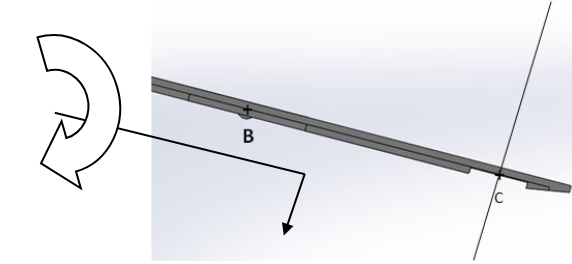
Solide en mouvement.
Ecrire que la somme des moments est nulle
Résoudre et valider ou invalider le sens imposé à l'action inconnue :
Comme le résultat de l'exemple en négatif cela veut dire que le sens que l'on c'est imposé pour est opposé à la réalité ainsi :
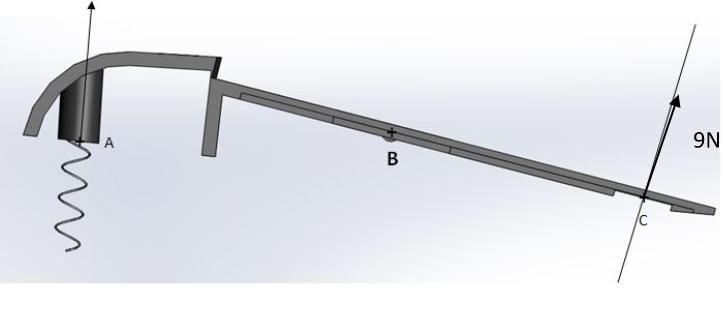
Solide en mouvement.
Cas plan générique
Dans le cas où les distances de bras de levier et orientations d'actions par rapport au bras de levier ne sont pas connus ou à partir de liaisons la méthode de calcul de moment précédente peut se compléter afin d'éviter de réaliser trop de calculs trigonométriques.
- On ne connait pas l'orientation par rapport à ni la distance : On souhaite calculer le moment en
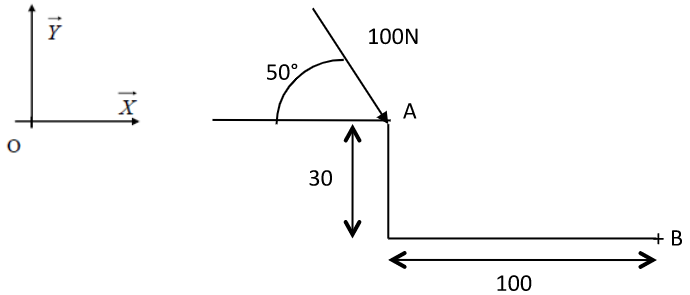
Schéma du problème.
On calcul le vecteur force : On décompose le problème en cas simples : avec chaque fois seulement la force en ou en
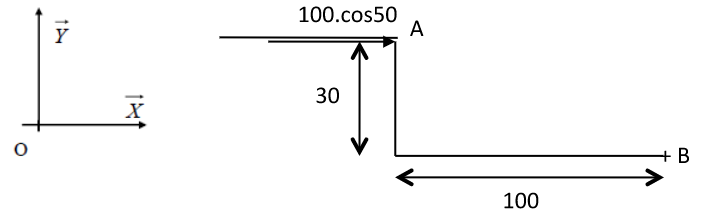
Cas simplifié avec seulement Fa sur x.
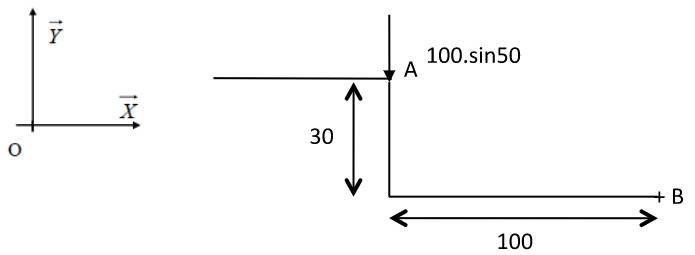
Cas simplifié avec seulement Fa sur y.
Le moment se calcul à chaque fois avec la distance mesurée perpendiculairement à l'effort :
Pour sur x : moment en
Pour sur y : moment en
Le moment de cette force en
On est en présence d'une liaison sans moment : On souhaite calculer le moment en
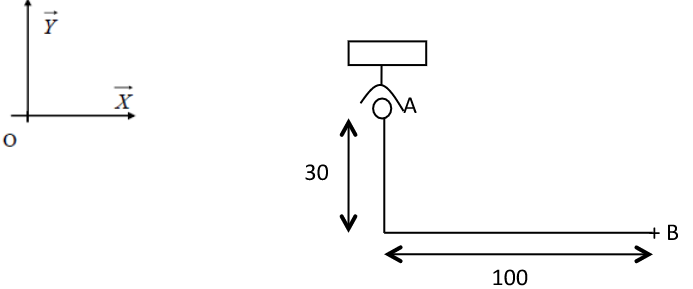
Schéma du problème.
On identifie d'abord le torseur d'actions transmissibles par la liaison :
| R | T |
|---|---|
Ensuite on écrit le torseur transmissible il suffit de remplacer les par des inconnues les par des : L'hypothèse plane donne car est la profondeur donc : On peut alors comme il n"y a pas de moment remplacer ce torseur par une force en : Et ensuite comme pour le cas précédent décomposer en deux cas simples sur puis .
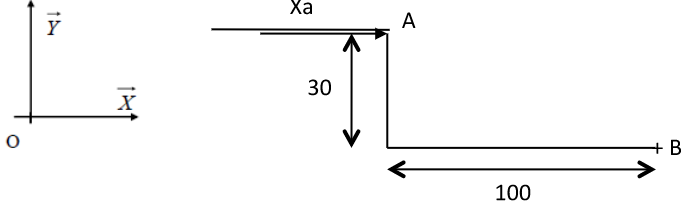
Cas simplifié avec seulement Fa sur x.
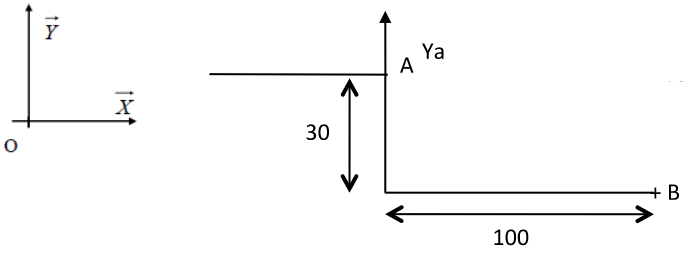
Cas simplifié avec seulement Fa sur y.
- On est en présence d'une liaison avec moment : On souhaite calculer le moment en B
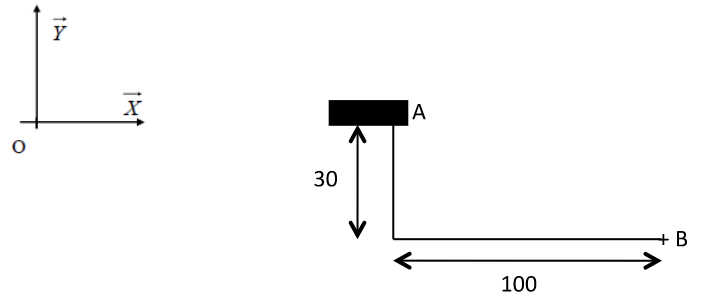
Schéma du problème.
On identifie d'abord le torseur d'actions transmissibles par la liaison :
| R | T |
|---|---|
Ensuite on écrit le torseur transmissible : L'hypothèse plane donne et car est la profondeur donc :
On peut alors remplacer temporairement ce torseur par une force en : mais à la fin du calcul du moment il faudra lui ajouter . Ici :
le moment de sur donne :
le moment de sur donne :
le moment à ne pas oublier du torseur est
Le moment en de cet encastrement est donc :
Commentaires
ZawaK
0
La réponse de la carte dépasse celle-ci
ZawaK
0
Ecris un commentaire..





