


Les Vecteurs
Vecteurs
Définition
Propriété
Soient et deux points du plan. La translation qui transforme en est la transformation qui associe à tout point du plan l'unique point tel que soit un parallélogramme (éventuellement aplati : les points , , et sont alignés) (voir figure ci-dessous)
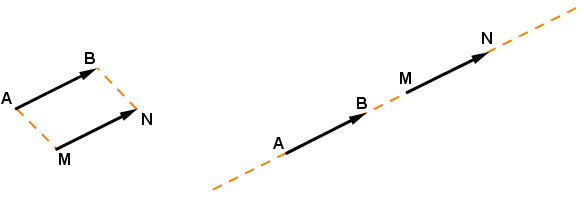
On dit alors que les points et (pris dans cet ordre) et que les points et (pris dans cet ordre) représentent la même translation associé à un seul vecteur noté ou . On écrit
Remarque
Un vecteur est défini par trois caractéristiques :
Sa direction : c'est la direction de la droite .
Son sens : c'est de vers .
Sa longueur, ou norme : c'est la distance . La norme se note . On a donc .
Égalité de deux vecteurs
Définition
On dit que deux vecteurs et sont égaux s'ils ont :
même direction (les droites et sont parallèles);
même sens (de vers comme de vers );
même longueur ( ). On écrit
Propriété
= si et seulement si est un parallélogramme.
si et seulement si les deux segments
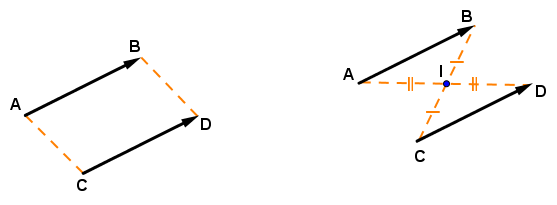
Vecteur nul
Définition
Le vecteur nul noté est le seul vecteur ayant une longueur égale à zéro ().
Pour tout point , on a .
Somme de deux vecteurs
Relation de Chasles
Propriété
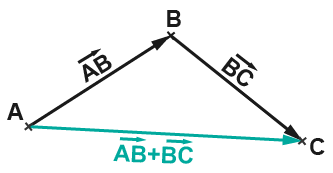
Construction de la somme de deux vecteurs
Propriété
Soient et deux vecteurs et un point quelconque du plan. La construction de la somme peut se faire de deux manières :
Méthode de Chasles : Il existe un unique point tel que et il existe un unique point tel que . Donc d’après la relation de Chasles (voir la figure ci-dessous) :
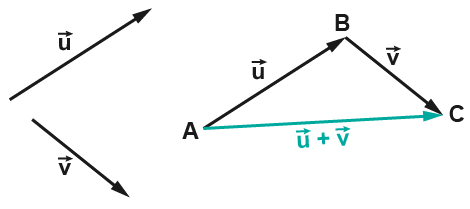
Méthode du parallélogramme : Il existe un unique point tel que et il existe un unique point tel que . La somme de et (c'est-à-dire de et ) est le vecteur tel que le quadrilatère est un parallélogramme (voir la figure ci-dessous).
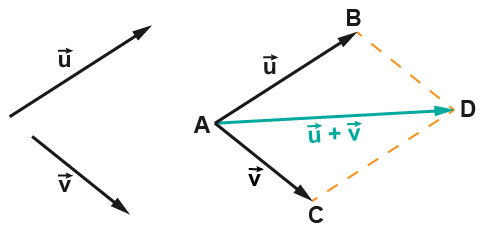
Conclusion : est un parallélogramme si et seulement si
Propriété
Pour tous vecteurs , et :
Vecteur opposé - Différence de deux vecteurs
Vecteur opposé
Définition
Soit un vecteur non nul.
Le vecteur opposés de noté , est le vecteur ayant la même direction, la même norme que , mais de sens opposés.
Propriété
L’opposé de est , c'est-à-dire .
Différence de deux vecteurs
Propriété
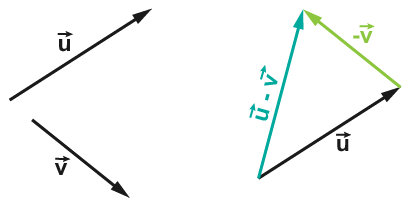
La différence de deux vecteurs et (notée ) est la somme de et de l'opposé de .
Multiplication d’un vecteur par un réel
Définition
Soient un vecteur et un nombre réel quelconque.
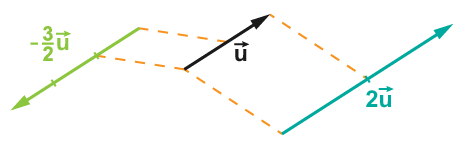
Le produit du vecteur par le nombre est le vecteur noté tel que :
Si alors et sont des vecteurs de même direction, de même sens et .
Si alors et sont des vecteurs de même direction, de sens contraire et ( est positif dans ce cas).
Propriété
Pour tous vecteurs et et pour tous nombres réels et :
si et seulement si ou
Colinéarité de deux vecteurs
Définition
On dit que deux vecteurs sont colinéaires s’ils ont la même direction.
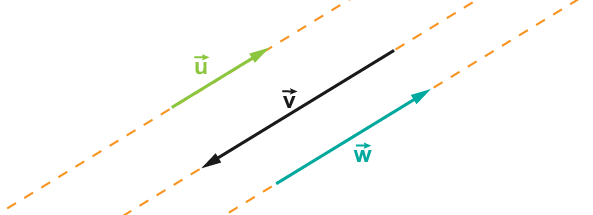
Les vecteurs , et sont colinéaires
Propriété
Deux vecteurs et sont colinéaires si et seulement s’il existe un réel tel que (On peut appeler , coefficient de colinéarité des deux vecteurs).
Points alignés - Droites parallèles
Propriété
Trois points , et sont alignés si et seulement si les vecteurs et sont colinéaires. C'est-à-dire : « , et sont alignés si et seulement s’il existe un réel tel que ».
Deux droites et sont parallèles si et seulement si les vecteurs et sont colinéaires. C'est-à-dire : « si et seulement s’il existe un réel tel que ».
Coordonnées d’un vecteur
Propriété
Le plan est muni d’un repère .
Pour tout vecteur , il existe un unique point du plan tel que : .
Les coordonnées du vecteur sont les coordonnées du point . On note ou .
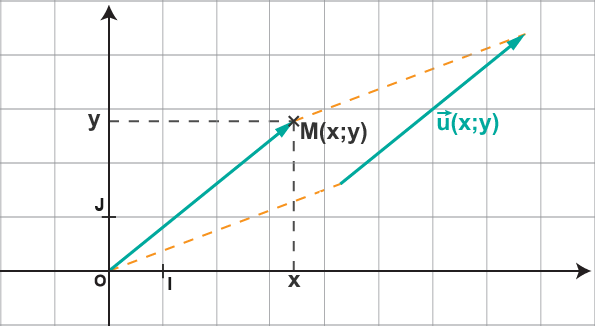
Propriété
Deux vecteurs sont égaux si et seulement s’ils ont les mêmes coordonnées.
Dans un repère , les coordonnées du vecteur tels que et , sont .
Propriété
Pour tous vecteurs et et pour tout nombre réel :
Les coordonnées du vecteur sont .
Les coordonnées du vecteur sont .
Propriété
Deux vecteurs et sont colinéaires si et seulement si :
Méthode 1 : .
Méthode 2 : il existe une réel tel que : et .

Mots clés à retenir : Vecteurs, Vecteurs colinéaires, Points alignés, Droites parallèles.
Commentaires
Jeanne.g
0
comment on trouve les coordonnés du milieu d'un vecteur ?
mathias pilote
-1
Ecris un commentaire..
mathias pilote
-1
Ecris un commentaire..
mathias pilote
-2
Ecris un commentaire..
mathias pilote
-2
Ecris un commentaire..
mathias pilote
-2
Ecris un commentaire..
kbyla
0
cool
thouguex
0
tres bonne video mercie! qui
ayoub
0
Ecris un commentaire..
Mimi21
0
super les exos !!!
jannaa
0
j'ai rien compris sur la colinéarité !!!
iyonna
0
merci pour tout sas mais je ne vois pas pourquoi les droites u,v et w sont colinéaire car ils n'ont pas le même sens et la direction je ne sais pas ce que c'est malgré que l'on m'explique car sinon toute les droites que je verrai sur ma feuille seront toute colinéaires
Marie
0
Merci pour le cours, mais je n'ai pas vraiment compris l'addition de vecteurs...
simoM74
1
j'ai beau revoire et revoire ce même chapitre avec des cours diférents je n'arive toujour pas a comprendre (de puis des semaines)
lol51350
-1
♥♥♥♥ C'est beaucoup plus intéressant que les cours des prof MERCI !!!
kenza
0
merci pour le cours mais je n'ai pas très bien compris comment on trouve les coordonnées d'un vecteur
Shaye
0
@iyonna : Les vecteurs u et v sont colinéaires car ils ont la même direction : direction = inclinaison des vecteurs. Avoir la même inclinaison (direction) pour deux droites ou vecteurs signifie qu'elles sont parallèles entre elles.
Le sens t'indique précisément le "lieu" de déplacement.
Pense à une autoroute qui relie Paris-Marseille, et une autoroute parallèle qui relierait Nantes à Bordeaux. Imagine que ce sont des lignes droites. Dans l'un des cas on peut soit aller de Paris vers Marseille (le sens est vers le bas) ou de Marseille vers Paris (sens vers le haut), dans l'autre cas on peut faire Nantes-Bordeaux (sens vers le bas) ou Bordeaux-Nantes (sens vers le haut).
En fonction de ton trajet le sens (vers le haut ou vers le bas) diffère et pourtant les 2 autoroutes ont la même direction car elles sont parallèles, elles sont donc colinéaires.
xxxl444
0
Superbe !
enzo a
1
comment on fait les exos
teva971
1
avec un stylo
RaphiX
0
j ais beacoup de difficulte a comrpendre ca
teva971
0
ou est la leçon sur les vecteur directeur?
asri
2
bonjour
asri
0
comment vat u
asri
0
merci pour vous
asri
1
mathrix
jeandogb
0
je n'ai pas bien compris la translation
jeandogb
0
je n'ai pas bien compris la translation





