


Fonctions du Second Degré et Polynômes
Fonction trinôme et forme canonique
Fonction trinôme
Définition
On appelle fonction polynôme du second degré à coefficients réels, toute fonction définie sur , pouvant se ramener à la forme réduite :
où , et sont des réels avec .
L'expression est encore appelée trinôme du second degré.
Exemple
Forme canonique
Définition
On appelle forme canonique de la fonction trinôme du second degré
l’écriture :
tels que et .
Exemple
On considère la fonction trinôme du second degré . Écrire sous sa forme canonique.
Solution
On a avec , et D’après la définition de la forme canonique :
α=−2ab=−2×23=−43
β=p(α)=p(−43)=2(−43)2+3(−43)−7=
Donc la forme canonique de la fonction trinôme est
Autre méthode pour calculer la forme canonique
Il suffit de construire une identité remarquable dans le trinôme :
RAPPEL : Pour tous nombres et :
Donc
Etude d'une fonction trinôme
Sens de variations et représentation graphique
Propriété
Soit une fonction trinôme de second degré définie par sa forme canonique : tels que , et sont trois nombres réels et .
Le sens de variation de dépend du signe de
Exemple
Donner le tableau de variation et tracer la courbe représentative de la fonction .
Même question pour la fonction .
Solution
Puisque alors est décroissante sur l’intervalle
puis croissante sur l’intervalle
Voici le tableau de variation et la courbe de :
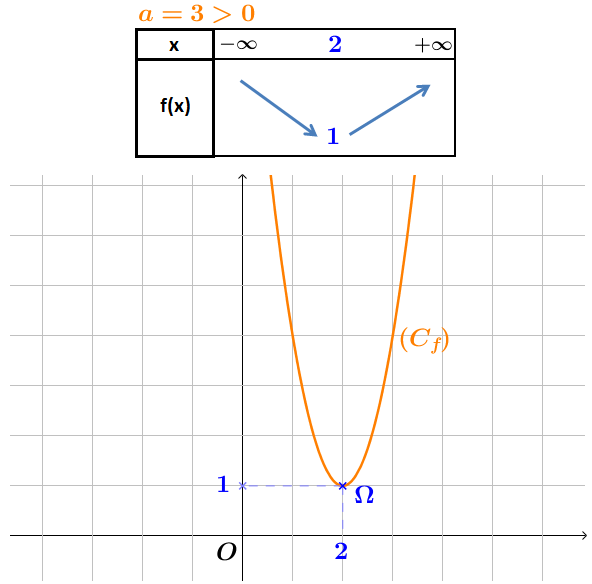
On écrit d’abord sous sa forme canonique :
Puisque alors est croissante sur l’intervalle () puis décroissante sur l’intervalle . Voici le tableau de variation et la courbe de :
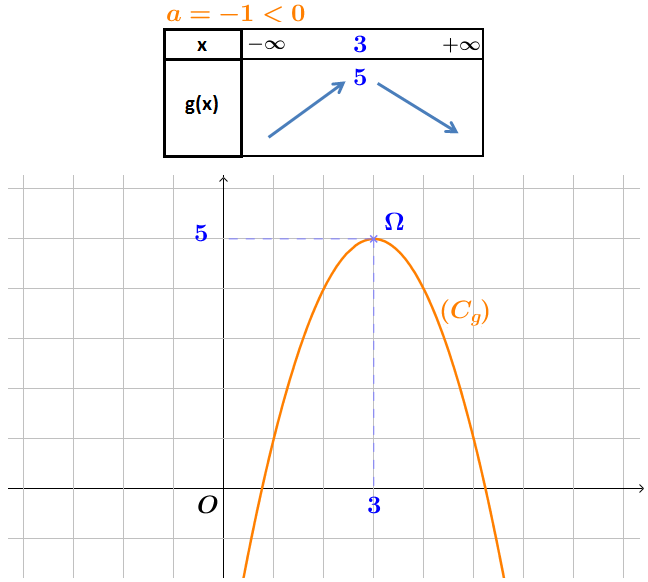
Extremum
Propriété
Soit une fonction trinôme de second degré définie par sa forme canonique : tels que , et sont trois nombres réels ().
La fonction admet comme extremum sur , atteint pour :
Si alors est un minimum.
Si alors est un maximum.
Exemple
Déterminer l’extremum de la fonction .
Solution
On a , et Puisque alors (c'est-à-dire ) est le minimum de sur , atteint en (c'est-à-dire ).
Signes
Propriété
Soit une fonction trinôme de second degré définie par sa forme canonique : tels que , et sont trois nombres réels ().
Si et , alors la fonction est positive sur
Si et , alors la fonction est négative sur .
Dans les autres cas ( et ont des signes différents), on utilise la forme factorisée de puis on dresse un tableau de signe.
Exemple
Etudier le signe des trois fonctions trinômes suivantes :
f(x)=(x−4)2+5
g(x)=−7(x+31)2−6
Solution
Signe de : pour tout
donc est positive sur .
Signe de : Pour tout :
donc est négative sur .
Signe de : On remarque ici que et (signes différents), dans ce cas il faut penser au tableau de signe de la fonction . Premièrement on factorise l’expression par l’identité remarquable :
Tableau de signe de (Voir le cours : « Factorisation et Etudes de Signe ») : si et seulement si . si et seulement si .

Conclusion : est positive sur l’ensemble et négative sur l’intervalle
Forme adaptée d'une fonction trinôme
Exemple
On considère la fonction trinôme définie par sa forme réduite
Vérifier que les deux formes suivantes (canonique et factorisée), sont celles de :
Selon la forme la plus adaptée, répondre aux questions suivantes :
Déterminer les coordonnées du sommet de la courbe de , puis donner son tableau de variation et déterminer son extremum sur .
Déterminer les éventuels antécédents de par .
Déterminer les éventuels antécédents de par .
Etudier le signe de .
Solution
On développe les deux expressions pour prouver qu’elles sont égales à :
Pour les coordonnées du sommet de la parabole, le tableau de variation et l’extremum de , la forme la plus adaptée est la forme canonique :
Le sommet de la parabole de est
Un premier item...
Un second...
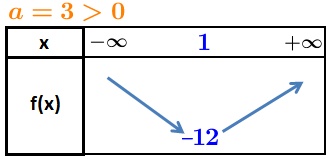
Texte alternatif
Pour déterminer les antécédents de , on résout l’équation , donc la forme la plus adaptée est la forme factorisée :

Les antécédents de sont et .
our déterminer les antécédents de , on résout l’équation , donc la forme la plus adaptée cette fois est la forme canonique :

Texte alternatif
Les antécédents de sont et
Pour étudier le signe de On utilise la forme factorisée . Revoir le paragraphe « signe d’une fonction trinôme » : Tableau de signe de : si et seulement si . si et seulement si .

Conclusion : est positive sur l’ensemble et négative sur l’intervalle

Mots clés à retenir : Forme canonique, Parabole, Sommet, Variations, Signe, Extremum.
Commentaires
Oumah
0
c'est très explicite. merci bcp
Oumah
-1
c'est très explicite. merci bcp
Oumah
0
c'est très explicite. merci bcp
Hichem
0
Ecris un commentaire..
eyashoko
1
Bonjour,
Dans la partie "Formes adaptée*s* d'une fonction trinôme", lors du calcul des antécédents de 6, dans la phrase de conclusion, les deux antécédents sont en fait les mêmes : il faudrait remplacer le signe de l'addition en soustraction, cela empêcherait la confusion chez certains ^^.
Merci bien !
Je sais pas si ma phrase était suffisemment claire xD=
eyashoko
0
suffisamment*
erreur de frappe c'est pas tellement évident sur mon pitit ordi-tablette
eyashoko
0
Quoi qu'il en soit merci pour ces leçons, je viens de m'inscrire et je viens de trouver exactement ce que je cherchais sur cette leçon thank u again
Mailysse
-2
bonjour, je cherche le cours sur les fonctions inverses. Est-ce-que qlq 1 peut m'aider
Mailysse
0
D'avance merci +++.
leaptvv
1
y'a une petit probleme avec le premier exemple





