Fonctions homographiques

Introduction

Dans ce chapitre, nous allons étudier le signe d'une fonction homographique. Une fonction homographique est un façon compliquée de dire un quotient de deux fonctions linéaires. Comme un division est équivalente à une multiplication par l'inverse, les règles pour déterminer le signe d'une fonction homographique vont être les mêmes que pour un produit de deux fonctions affines, avec une exception: il faudra exclure la valeur annulatrice de $cx+d$ du domaine de définition de $f$ .

Ecrivons ce qu'on vient de dire mathématiquement:

Définition

Soient $a$ , $b$ , $c$ et $d$ quatre nombres réels tels que $c \neq 0$ .

La fonction $f$ définie par : $f(x)= \dfrac{ax+b}{cx+d}$ est appelée fonction homographique.

On remaquera que diviser $ax+b$ par $cx + d$ est équivalent de multiplier deux fonctions affines $ax+b$ et $\dfrac{1}{cx+d}$ . Passons maintenant à la valeur qui annule le dénominateur, c'est-à-dire $cx+d$ .

Domaine de définition d’une fonction homographique

Regardons maintenant comment calculer la valeur interdite et écrire le domaine de définition à partir de celle-ci:

Propriété

Soit la fonction homographique $f(x)= \dfrac{ax+b}{cx+d}$ et $D_f$ son ensemble de définition.

La fonction $f$ n’est pas définie en la valeur où s’annule le dénominateur, c'est-à-dire où $cx+d = 0$ . Donc pour $cx = -d$ ou $x = -\dfrac {d}{c}$ .

Le domaine de définition de $f$ est donc: $D_f = \mathbb{R} \backslash \{ -\dfrac {d}{c}\}$ , et $-\dfrac {d}{c}$ est appelée la valeur interdite.

Faisons un exemple introductif:

Exemple

Déterminer l’ensemble de définition de la fonction $f(x) =\dfrac{5x-4}{3x+12}$ .

Solution

Il suffit de calculer la valeur interdite : On voit que $c=3$ et $d=12$ , donc

-\frac d c = -\frac {12} 3 = -4

d’où $D_f = \mathbb{R} \backslash \{-4\}$ .

On peut aussi résoudre l’équation $3x+12=0$ .

\begin{aligned} &3x+12=0\\ &3x=-12\\ &x=\frac {-12} 3=-4. \end{aligned}

On retrombe donc sur $D_f = \mathbb{R} \backslash \{-4\}$ .

Tableau de signes d’une fonction homographique

Pour déterminer le signe d’une fonction homographique, on utilise exactement la même méthode que pour un produit de fonctions affines, sans oublier de calculer et de noter la valeur interdite. La méthode est la suivante:

Calculer la valeur qui annule $ax+b$ . Tracer sur la première ligne le tableau de signes du premier terme $ax+b$ , ainsi que sa valeur annulatrice.
Calculer la valeur qui annule $cx+d$ . Sur la deuxième ligne, tracer le tableau de signes du second terme $cx+d$ , ainsi que sa valeur interdite.
Sur la troisième ligne, le signe du produit $(ax+b)(cx+d)$ s'obtient par l'application de la règle des signes de haut en bas $\downarrow$ .

Attention : La fonction homographique n’est pas définie en la valeur interdite, on met un double trait au niveau de cette valeur dans la dernière ligne du tableau de signe.

Faisons maintenant quelques exemples pour tester la méthode:

Exemple

Dresser un tableau de variation de ces deux fonctions homographiques:

\frac{x-2}{3x-9} \qquad ; \qquad \frac{4x+1}{1-x}

Solution

Commencons par $\dfrac{x-2}{3x-9}$ :

On détermine la valeur où s’annule $x-2$ : $x-2=0$ équivaut à $x=2$ .
On détermine la valeur où s’annule $3x-9$ : $3x-9=0$ équivaut à $3x=9$ équivaut à $x=\dfrac{9}{3} =3$ .
On fait apparaître dans un tableau de signes, les signes de $x-2$ et de $3x-9$ , puis on utilise la règle des signes pour en déduire le signe du quotient $\dfrac{x-2}{3x-9}$ :

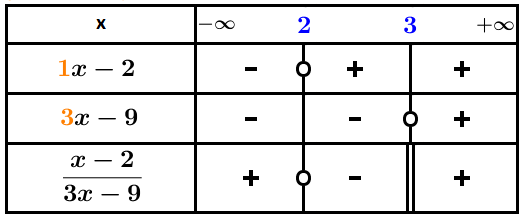
Pour l’expression $\dfrac{4x+1}{1-x}$ :

On détermine la valeur où s’annule $4x+1$ : $4x+1=0$ équivaut à $4x=-1$ équivaut à $x={-\dfrac{1}{4}}$ .
On détermine la valeur où s’annule $1-x$ : $1-x=0$ équivaut à $x= {1}$ .
On dresse le tableau de signes du quotient $\dfrac{4x+1}{1-x}$ :

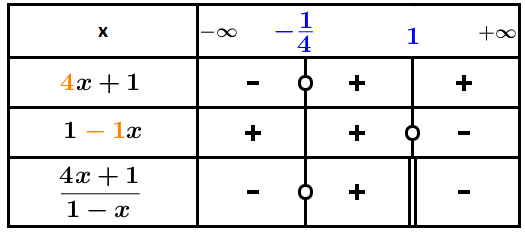
Revenir au chapitre

Déterminer le signe d'une fonction affine

Signe d'une fonction homographique

Factoriser avec le Facteur Commun

Factoriser avec les Identités Remarquables

Fonctions homographiques

Introduction

Définition

Domaine de définition d’une fonction homographique

Propriété

Exemple

Tableau de signes d’une fonction homographique

Exemple

Yasse

Classes

Entreprise

Réseaux sociaux