Factorisation et Etude de Signe

Signe d’une fonction affine

Propriété

On considère deux réels $a$ et $b$ ( $a\neq 0$ ).

La fonction affine définie sur $\mathbb{R}$ par $f(x) = ax + b$ , s’annuleet change de signe une seule fois au point $x_0=- \dfrac b a$ .

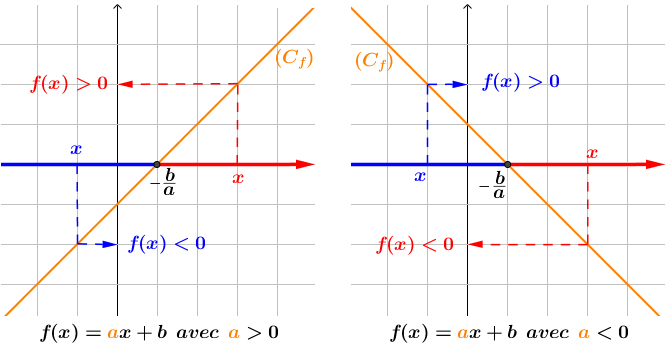
Courbe d’une fonction affine selon le signe de aa

Propriété

Le signe de la fonction $x \longmapsto ax + b$ suivant la valeur de $x$ est donné par le tableau ci-dessous :

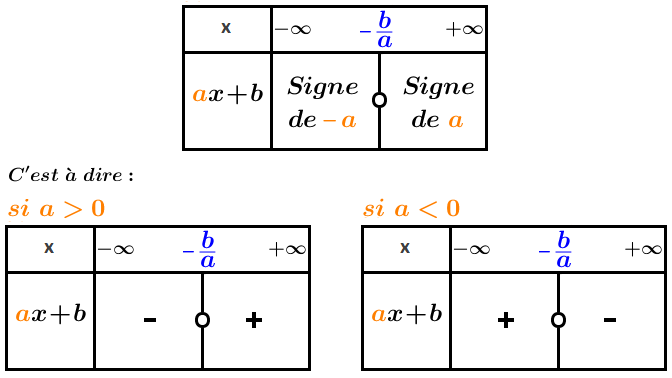
Tableau de signe d’une fonction affine selon le signe de $a$

Exemple

Donner le tableau de signe des deux fonctions affine

x⟼2x−6
Un second...

Solution

Étudions le signe de $2x-6$ Premièrement, on cherche la valeur où s’annule $2x-6$ . On résout donc l’équation $2x-6=0$ :

2x - 6 = 0 \\ 2x= 6 \\ x = \frac{6}{2} = 3

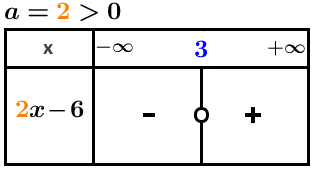
Étudions le signe de $-3x + 5$

-3x + 5 = 0 \\ -3x = -5 \\ x = \frac{-5}{-3} = \frac{5}{3}

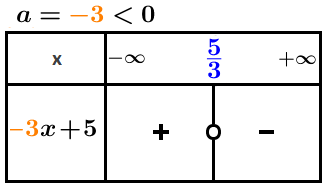
Factorisation

Factoriser en cherchant un facteur commun

Propriété

Pour tous nombres réels $a$ , $b$ et $k$ :

ka+kb=k(a+b).

( ${\color{green}k}$ est appelé facteur commun.)

Exemple

Factorisons les expressions

3x2−2x
(5x+1)(7x−2)+(5x+1)(x+1)

Solution

Le facteur commun pour l’expression $3x^2-2x$ est ${\color{green}x}$

3x^{2} −2x=x(3x−2).

Le facteur commun pour l’expression

(5x+1)(7x−2)+(5x+1)(x+1)

est ${\color{green}5x+1}$ :

(5x+1)(7x−2)+(5x+1)(x+1) ​ =(5x+1)((7x−2)+(x+1))\\ =(5x+1)(7x−2+x+1) =(5x+1)(8x−1)

Factoriser en utilisant les identités remarquables

Propriété

Pour tous nombres réels $a$ et $b$ :

​ a^{2} - b =(a−b)(a+b) \\ a^{2} +2ab+b^{2} = (a+b)^{2}\\ a^{2} - 2ab+b^{2} = (a−b) ^{2} . ​

Exemple

Factorisons les expressions

x2−25
x2−5

Solution

D’après la première identité remarquable :

x^{2} −25 = x^{2} - 5 ^{2}\\ = (x-5)(x+5)

D’après la première identité remarquable :

x^{2} - 5 = x^{2} - \sqrt{5}^{2} \\ =(x− \sqrt{5} )(x+ \sqrt{5} ). ​

D’après la troisième identité remarquable :

x^{2}−6x+9 = x^{2} -2×3×x+3^{2}\\ =(x−3)^{2} . ​

Signe du produit de deux fonctions affines

Propriété (règle des signes)

Propriété

Le produit (ou quotient) de deux nombres de même signeest positif.

Exemple

5×4=20;(−3)×(−2)=6.

Propriété

Le produit (ou quotient) de deux nombres de signes contraires est négatif.

Exemple

(−6)×2=−12;8×(−3)=−24.

Méthode (Signe du produit de deux fonctions affines)

Pour déterminer le signe du produit de deux fonctions affines, on dresse un tableau dans lequel le signe de chacun des facteurs apparaît sur une ligne. Le signe du produit s'obtient sur la dernière ligne en appliquant la règle des signes.

Exemple

Résoudre l’inéquation $(x-1)(2x-6) \leq 0$ .
Résoudre l’inéquation $(1-2x)(3x+4)<0$ .

Solution

Pour résoudre l’inéquation $(x-1)(2x-6) \leq 0$ On dresse le tableau de signe de l’expression $(x-1)(2x-6)$ :

On détermine la valeur où s’annule $x-1$ :
$x-1=0$ équivaut à $x={\color{purple}1}$ .
On détermine la valeur où s’annule $2x-6$ :
$2x-6=0$ équivaut à $2x=6$ équivaut à $x=\dfrac{6}{2} = {\color{purple}3}$ .
On fait apparaître dans un tableau de signes, les signes de $x-1$ et de $2x-6$ , puis on utilise la règle des signes pour en déduire le signe du produit $(x-1)(2x-6)$ :

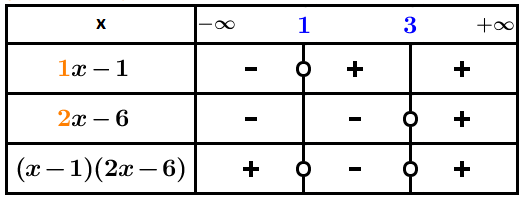
Conclusion : D’après le tableau, Les solutions de l’inéquation $(x-1)(2x-6) \leq 0$ sont les valeurs de l’intervalle $[1 ; 3]$ .On écrit : $S=[1 ; 3].$ ( $S$ est l’ensemble de solutions)

On dresse le tableau de signe de l’expression $(1-2x)(3x+4)$ :

On détermine la valeur où s’annule $1-2x$ :
$1-2x=0$ équivaut à $-2x=-1$ équivaut à $x=\dfrac{-1}{-2}={\color{purple}\dfrac{1}{2}}$ .
On détermine la valeur où s’annule $3x+4$ :
$3x+4=0$ équivaut à $3x=-4$ équivaut à $x={\color{purple}-\dfrac{4}{3}}$ .
On dresse le tableau de signes du produit $(1-2x)(3x+4)$ :

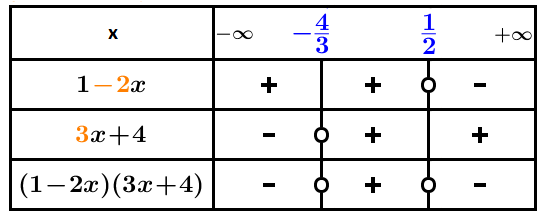
D’où les solutions de l’inéquation $(1-2x)(3x+4) < 0$ sont les valeurs des deux intervalles $\left]-\infty ; -\dfrac{4}{3} \right[$ et $\left] \dfrac{1}{2} ; +\infty \right[$ .

C’est à dire : $S=\left]-\infty ; -\dfrac{4}{3} \right[\bigcup\left] \dfrac{1}{2} ; +\infty \right[$ . ( $\cup$ se lit union)

Signe d’une fonction homographique

Fonction homographique

Définition

Soient $a$ , $b$ , $c$ et $d$ quatre nombres réels tels que $c \neq 0$ .

La fonction $f$ définie par : $f(x)= \dfrac{ax+b}{cx+d}$ est appelée fonction homographique.

Domaine de définition d’une fonction homographique

Propriété

Soit la fonction homographique $f(x)= \dfrac{ax+b}{cx+d}$ et $D_f$ son ensemble de définition. La fonction $f$ n’est pas définie en la valeur où s’annule le dénominateur : $cx+d = 0$ équivaut à $cx = -d$ équivaut à $x = {\color{purple}-\dfrac d c }$ . donc $D_f = \mathbb{R} \backslash \{{\color{purple}-\dfrac d c } \}$ .
${\color{purple}-\dfrac d c}$ est appelée la valeur interdite

Exemple

Déterminer l’ensemble de définition de la fonction $f(x) =\dfrac{5x-4}{3x+12}$ .

Solution

Il suffit de calculer la valeur interdite : On voit que $c=3$ et $d=12$ , donc

− \frac{d}{c} = - \frac{12}{3} = -4​

d’où $D_f = \mathbb{R} \backslash \{ {\color{purple}-4}\}$ .

3x+12=0\\ 3x=−12\\ x= -\frac{12}{4}\\ =−4.\\ ​

Donc $D_f = \mathbb{R} \backslash \{ {\color{purple}-4}\}$ .

Pour déterminer le signe d’une fonction homographique, on dresse un tableau dans lequel on fait apparaître le signe du numérateur et du dénominateur. Le signe du quotient s'obtient sur la dernière ligne en appliquant la règle des signes.

Attention : La fonction homographique n’est pas définie en la valeur interdite, on met un double trait au niveau de cette valeur dans la dernière ligne du tableau de signe (voir les exemples).

Exemple

Résoudre les inéquations

\frac{x-2}{3x-9} \geq 0 ; \frac{4x+1}{1-x} < 0

Solution

L’expression $\dfrac{x-2}{3x-9}$ est le quotient des deux expressions affines $x-2$ et $3x-9$ .

On détermine la valeur où s’annule $x-2$ :
$x-2=0$ équivaut à $x={\color{purple}2}$ .
On détermine la valeur où s’annule $3x-9$ :
$3x-9=0$ équivaut à $3x=9$ équivaut à $x=\dfrac{9}{3} ={\color{purple}3}$ .
On fait apparaître dans un tableau de signes, les signes de $x-2$ et de $3x-9$ , puis on utilise la règle des signes pour en déduire le signe du quotient $\dfrac{x-2}{3x-9}$ :

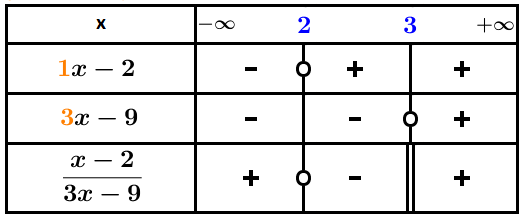
D’où les solutions de l’inéquation $\dfrac{x-2}{3x-9} \geq 0$ sont les valeurs des deux intervalles $\rbrack-\infty ; 2\rbrack$ et $\rbrack 3 ; +\infty [$ .

D’où $S= \rbrack-\infty ; 2\rbrack \cup \rbrack 3 ; +\infty [$ .

Attention: On ouvre le crochet en ${\color{purple}3}$ parce que la fonction $x \longmapsto \dfrac{x-2}{3x-9}$ n’est pas définie en ${\color{purple}3}$ ( $3$ est la valeur interdite de la fonction).

Pour l’expression $\dfrac{4x+1}{1-x}$

On détermine la valeur où s’annule $4x+1$ :
$4x+1=0$ équivaut à $4x=-1$ équivaut à $x={\color{purple}-\dfrac{1}{4}}$ .
On détermine la valeur où s’annule $1-x$ :
$1-x=0$ équivaut à $x= {\color{purple}1}$
On dresse le tableau de signes du quotient $\dfrac{4x+1}{1-x}$

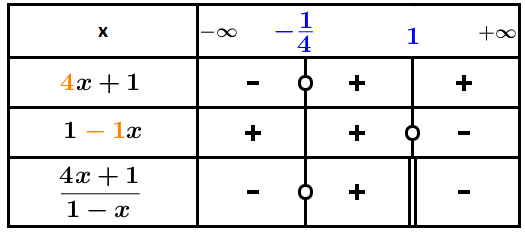
D’où les solutions de l’inéquation $\dfrac{4x+1}{1-x} >0$ sont les valeurs de l’intervalle $\rbrack-\dfrac 1 4 ; 1 [$ .

D’où $S = \rbrack-\dfrac 1 4 ; 1 [$ .

Activité

On considère l’inéquation $(I) : x^2-9 \geq 0$ .

Factoriser l’expression $x^2-9$ .
On déduire le tableau de signe de $x^2-9$ .
On déduire les solutions de l’inéquation $(I)$ .

Pour la solution, vous pouvez poser vos questions dans les commentaires.

Mots clés à retenir : Signe, Fonction affine, Fonction homographique, Produit, Quotient, Tableau de signe, Inéquation.

Factorisation et Etude de Signe

Signe d’une fonction affine

Propriété

Propriété

Exemple

Factorisation

Factoriser en cherchant un facteur commun

Propriété

Exemple

Factoriser en utilisant les identités remarquables

Propriété

Exemple

Signe du produit de deux fonctions affines

Propriété (règle des signes)

Propriété

Exemple

Propriété

Exemple

Méthode (Signe du produit de deux fonctions affines)

Exemple

Signe d’une fonction homographique

Fonction homographique

Définition

Domaine de définition d’une fonction homographique

Propriété

Exemple

Exemple

Activité

GL34_

Classes

Entreprise

Réseaux sociaux